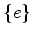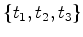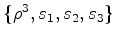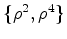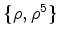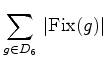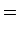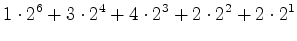|
|
|
|
- Quantos padrões
de colares
existem com 6 pérolas brancas ou
pretas?
O que é um padrão de colar?
Imaginemos que
as pérolas ocupam
os vértices de um hexágono
regular. Consideramos de novo o
conjunto
das colorações 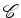 dos vértices, usando duas cores - branco e preto.
Já sabemos que existem as 64 colorações seguintes:
dos vértices, usando duas cores - branco e preto.
Já sabemos que existem as 64 colorações seguintes:
|
|
|
|
|
|
- No entanto agora a relação de
equivalência é
diferente - duas colorações
dizem-se equivalentes quando uma pode obter-se
a partir da outra por acção de um elemento do grupo das
simetrias do
hexágono - o chamado grupo
diedral
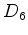 .
.
- Mais uma vez uma classe de
equivalência de colares coloridos diz-se um padrão.
O conjunto dos padrões é pois:
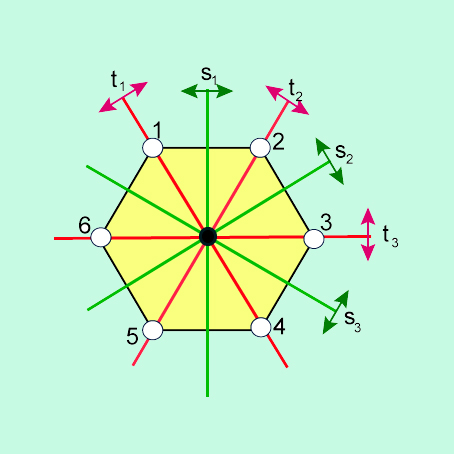
- O grupo diedral
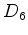 contem, para além das
rotações
consideradas
na secção anterior, as simetrias relativamente às
rectas indicadas
na figura seguinte. contem, para além das
rotações
consideradas
na secção anterior, as simetrias relativamente às
rectas indicadas
na figura seguinte.
|
|
|
|
|
|
Estas simetrias representam as
rotações espaciais de 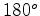 (em
torno dessas mesmas rectas, que dão a volta ao colar).
(em
torno dessas mesmas rectas, que dão a volta ao colar).
Portanto:
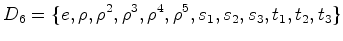 |
(10) |
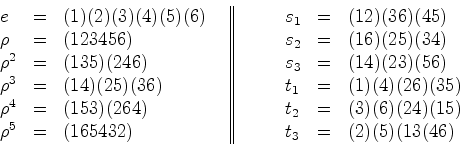
- O leitor pode verificar
como
exercício que a
representação destes
elementos como permutações dos vértices do
hexágono e a respectiva
decomposição em ciclos disjuntos é a seguinte:
- O problema
agora é calcular
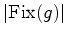 para
cada para
cada 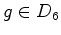 para
podermos aplicar
o lema de Burnside e calcular assim o número de padrões
de colares com 6 pérolas brancas e pretas. para
podermos aplicar
o lema de Burnside e calcular assim o número de padrões
de colares com 6 pérolas brancas e pretas.
|
|
|
|
|
|
|
|
|
|
|
|
Em geral, se 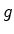 se
decompõe em se
decompõe em 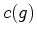 ciclos
disjuntos, o número de
colorações invariantes sob a acção de ciclos
disjuntos, o número de
colorações invariantes sob a acção de 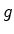 é é 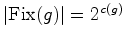 .
.
Da tabela anterior vemos que
existe:
1
|
permutação |
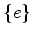 |
composta por |
6 |
ciclos |
| 3 |
permutações |
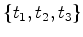 |
compostas por |
4 |
ciclos |
| 4 |
permutações |
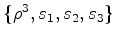 |
compostas por |
3 |
ciclos |
| 2 |
permutações |
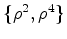 |
compostas por |
2 |
ciclos |
| 2 |
permutações |
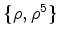 |
compostas por |
1 |
ciclo |
Portanto:
e, pelo lema de Burnside o
número de padrões pretendido é:
uma vez que 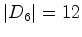 .
.
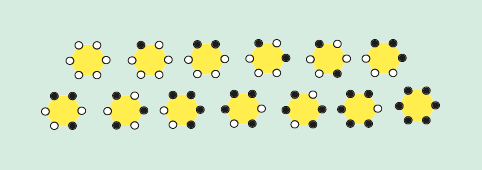
Existem
pois  padrões de colares distintos com 6 pérolas
brancas e pretas representados na figura seguinte (um colar
representativo de cada padrão):
padrões de colares distintos com 6 pérolas
brancas e pretas representados na figura seguinte (um colar
representativo de cada padrão):
|
|
|
|
|
|
|
|
|
Página
seguinte
Página anterior
Índice |
|
|
|
|

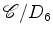
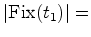 número de colorações
número de colorações 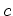 que ficam
invariantes sob a
acção da simetria
que ficam
invariantes sob a
acção da simetria 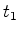 .
.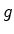 se
decompõe em
se
decompõe em 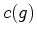 ciclos
disjuntos, o número de
colorações invariantes sob a acção de
ciclos
disjuntos, o número de
colorações invariantes sob a acção de 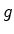 é
é 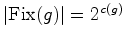 .
.
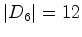 .
.
 padrões de colares distintos com 6 pérolas
brancas e pretas representados na figura seguinte (um colar
representativo de cada padrão):
padrões de colares distintos com 6 pérolas
brancas e pretas representados na figura seguinte (um colar
representativo de cada padrão):
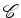
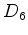
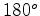 (em
torno dessas mesmas rectas, que dão a volta ao colar).
(em
torno dessas mesmas rectas, que dão a volta ao colar). 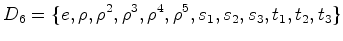
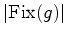 para
cada
para
cada 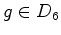 para
podermos aplicar
o lema de Burnside e calcular assim o número de padrões
de colares com 6 pérolas brancas e pretas.
para
podermos aplicar
o lema de Burnside e calcular assim o número de padrões
de colares com 6 pérolas brancas e pretas.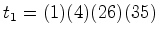 , o que significa que
, o que significa que 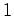 e
e 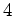 e permuta os vértices
e permuta os vértices 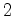 com
com 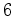 e
e 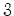 com
com 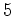 -
- 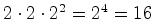 .
.