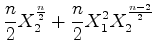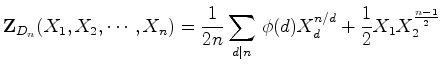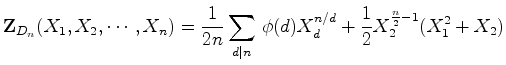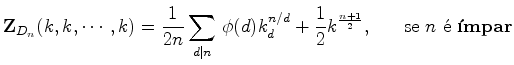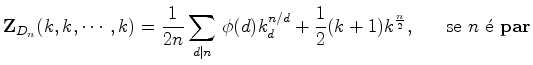O índice de ciclos de um grupo de permutações
|
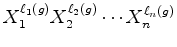
|
|||||||||||||||||||||||||||||||||||||||||
|
Exemplo 1
Índice de ciclos do grupo das rotações 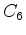 do
hexágono regular: do
hexágono regular:
Portanto o índice de ciclos de 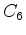 é o
polinómio: é o
polinómio: |
|||||||||||||||||||||||||||||||||||||||||
|
Exemplo 2
Índice de ciclos do grupo diedral 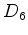 :
:
Portanto o índice de ciclos de 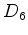 é o
polinómio: é o
polinómio:
|
|||||||||||||||||||||||||||||||||||||||||
|
Generalizando:
Cálculo
do
índice de ciclos do grupo diedral
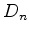
O grupo diedral 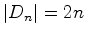 É constituído por 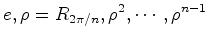 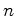 reflexões relativamente a rectas.
reflexões relativamente a rectas.
Para cada
Assim por exemplo, quando
Fixemos Agrupemos as rotações
 Para cada divisor A contribuição das
Concluindo: O índice
de
ciclos do grupo diedral
|
|||||||||||||||||||||||||||||||||||||||||
|
Em particular, o número de
colares
com
e:
Se 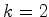 cores e
cores e 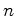 é um número primo
ímpar, o
número padrões de colares é:
é um número primo
ímpar, o
número padrões de colares é:
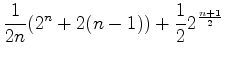
|
|||||||||||||||||||||||||||||||||||||||||
|
Mais exemplos de índices de ciclos: 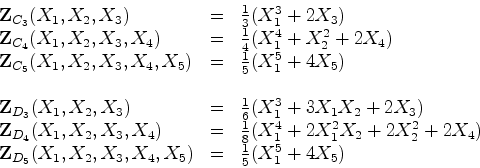
|
|||||||||||||||||||||||||||||||||||||||||
| Página
seguinte Página anterior Índice |
|||||||||||||||||||||||||||||||||||||||||
 seja
seja 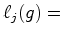
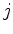
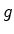
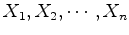 :
: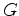
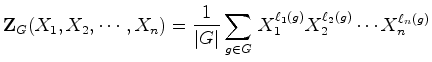
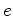
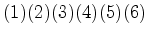
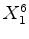
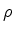
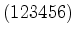
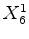
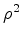
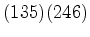

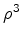
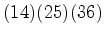
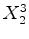
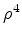

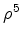
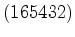
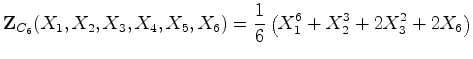
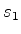
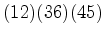
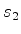
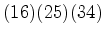
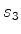

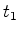
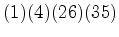
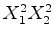
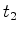
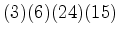
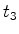
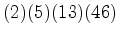
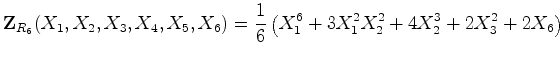
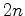 :
: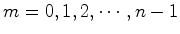 , a rotação
, a rotação 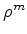 quando actua
nos
vértices
quando actua
nos
vértices 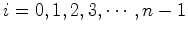 do
polígono regular de
do
polígono regular de 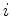 no vértice
no vértice 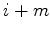 (módulo
(módulo 
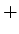
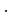
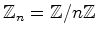
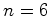 e
e 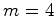 :
: 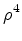
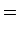
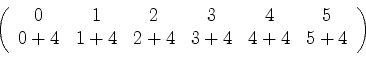
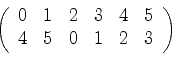
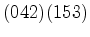
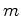 . Se
. Se 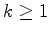 é o
menor
inteiro tal que
é o
menor
inteiro tal que 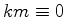 (mod
(mod 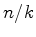 ciclos de comprimento
ciclos de comprimento  . Por outro lado, se
. Por outro lado, se 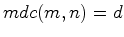 esse
inteiro
esse
inteiro 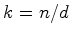 e portanto
e portanto 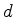 ciclos de
comprimento
ciclos de
comprimento 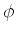 de Euler:
de Euler: 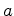
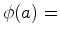

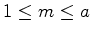
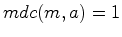
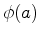
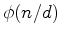 números
números 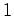 e
e 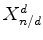 para o índice
de ciclos.
para o índice
de ciclos. 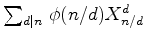 e,
em particular,
o
índice de ciclos do grupo
cíclico
e,
em particular,
o
índice de ciclos do grupo
cíclico 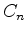 é:
é: 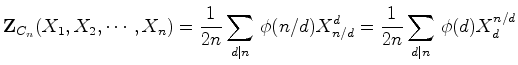
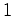 e
e
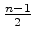 ciclos
de comprimento
ciclos
de comprimento 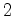 . A contribuição total para o índice de ciclos das
. A contribuição total para o índice de ciclos das
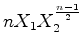
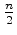 ciclos de comprimento
ciclos de comprimento 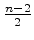 ciclos de
comprimento
ciclos de
comprimento