Next: Nomogramas
de cruzamento para ...
Índice
Nomogramas são gráficos que servem para
representar no plano, equações com várias
variáveis, de tal forma que o cálculo das suas
soluções se
reduz a uma simples leitura efectuada nesse gráfico. A
Nomografia ou Teoria dos Ábacos foi desenvolvida essencialmente
por Maurice d'Ocagne
em fins do século XIX.
Para uma perspectiva
histórica recente consultar H.
A. EVESHAM "Origins and
Development of Nomography", Annals of the History of Computing,
Volume
8, Number 4, October 1986.
Consideremos por exemplo a
equação com três variáveis  :
 |
(1) |
que nos
dá o resultado 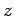 do produto de dois números do produto de dois números 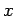 e e 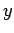 . .
Para construir um nomograma para esta equação, podemos
começar por representar,
relativamente a um sistema de eixos cartesianos 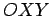 , as rectas  e  e ainda as curvas de
nível  (  e 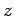 constantes) (ver a figura 1).
Figura 1: Nomograma da multiplicação
 |
Dados os valores das
variáveis  e e  , digámos , digámos 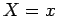 e e 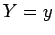 , o valor da
terceira variável , o valor da
terceira variável  , para o qual o triplo , para o qual o triplo  satisfaz a
equação dada (1), isto
é, satisfaz a
equação dada (1), isto
é,  , será o
nível , será o
nível 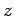 da curva de nível que passa pelo
ponto de intersecção das rectas da curva de nível que passa pelo
ponto de intersecção das rectas 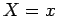 e e 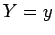 (ver a figura 1, onde representámos
a solução (ver a figura 1, onde representámos
a solução  ). ).
É claro que há outras opções. Podemos, por
exemplo,
representar, relativamente a um sistema de eixos cartesianos  , as rectas , as rectas  e e  e ainda as curvas de
nível correspondentes a valores constantes de e ainda as curvas de
nível correspondentes a valores constantes de  , digámos , digámos 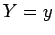 ,
isto é, o conjunto dos pontos ,
isto é, o conjunto dos pontos  tais que tais que  ( ( e
e 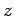 constantes). É claro que
estas curvas são as rectas constantes). É claro que
estas curvas são as rectas  no plano no plano  , que passam na origem e têm declive , que passam na origem e têm declive 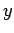 . A
leitura da solução . A
leitura da solução  faz-se por um processo
análogo ao
anterior - essa solução corresponde ao ponto de
intersecção das
rectas faz-se por um processo
análogo ao
anterior - essa solução corresponde ao ponto de
intersecção das
rectas 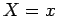 , ,  e e  (ver a figura 2, onde
representámos a solução (ver a figura 2, onde
representámos a solução
 ). ).
Figura 2: Nomograma para a multiplicação
 |
No applet seguinte, construído com o programa Cinderella,
representámos este segundo nomograma para a
multiplicação, usando
no entanto escalas diferentes para as variáveis. No applet
seleccione com o rato o valor de 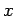 , e a inclinação , e a inclinação 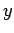 da recta da recta  . O valor do
produto . O valor do
produto  lê-se no
eixo lê-se no
eixo  ,
correspondente à recta ,
correspondente à recta  que intersecta o ponto de encontro
das duas rectas que intersecta o ponto de encontro
das duas rectas 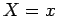 e e  . .
Esta última representação tem claramente
a vantagem, sobre a primeira, de que o nomograma é
constituído apenas por linhas rectas o que, para além de
ser mais fácil
de construir, permite uma leitura mais simples.
Podemos ainda obter um
nomograma rectilíneo (constituído
apenas por linhas rectas) para a equação (1),  , por um outro
processo. De facto essa equação pode
também ser escrita (para valores positivos das variáveis)
na
forma: , por um outro
processo. De facto essa equação pode
também ser escrita (para valores positivos das variáveis)
na
forma:
 |
(2) |
Relativamente a um sistema de eixos cartesianos 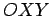 , pômos
então  , isto é,
usámos escalas logarítmicas nos eixos  e  , e considerámos as curvas de ní
vel correspondentes a valores constantes de  ,  , isto é, as
linhas rectas  (ver a figura 3, onde
representámos a solução
 )
Figura 3: Nomograma para a
multiplicação
 |
A anamorfose (ou rectificação) de um nomograma
consiste em
transformá-lo num nomograma rectilíneo,
constituído por três famílias de linhas rectas, que
se intersectam transversalmente, e indexadas pelos valores de 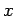 , , 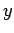 e e 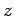 , respectivamente. A solução , respectivamente. A solução  da equação
dada será pois representada pelo ponto de
intersecção das três rectas indexadas por da equação
dada será pois representada pelo ponto de
intersecção das três rectas indexadas por  (ver a figura 4, onde representámos a
solução (ver a figura 4, onde representámos a
solução
 ). ).
Figura 4
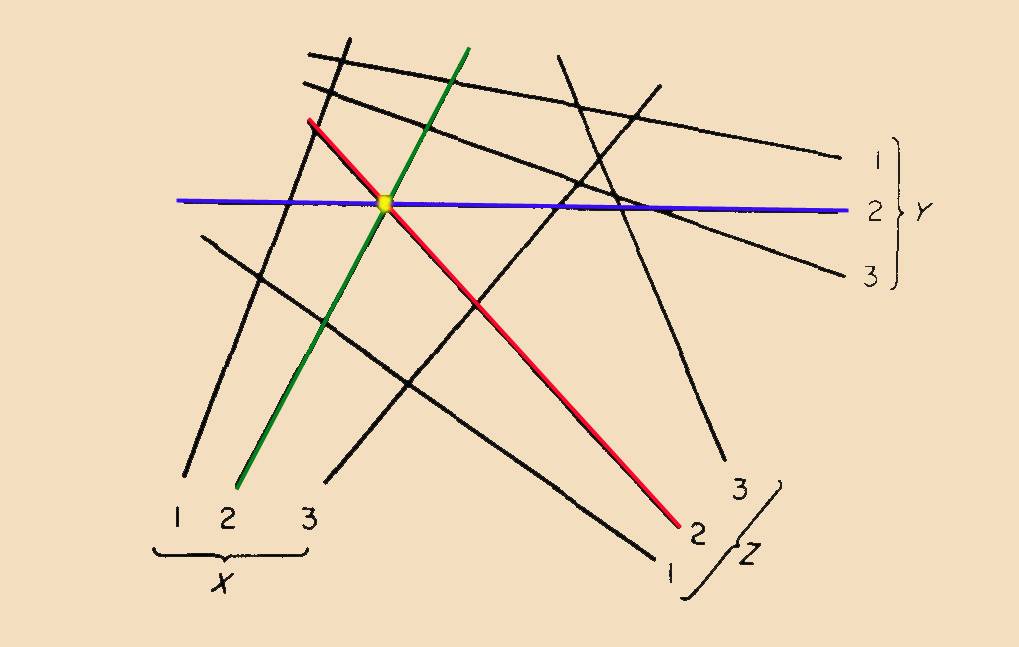 |
As linhas rectas de cada
família não são necessàriamente
paralelas entre si. Quando isto acontece os nomogramas dizem-se
paralelos e a anamorfose diz-se paralela.
Next: Nomogramas
de cruzamento para
Índice
Joao Nuno Tavares
2005-03-28
|

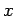 ,
, 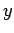 e
e 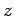 , respectivamente. A solução
, respectivamente. A solução  da equação
dada será pois representada pelo ponto de
intersecção das três rectas indexadas por
da equação
dada será pois representada pelo ponto de
intersecção das três rectas indexadas por  (ver a figura 4, onde representámos a
solução
(ver a figura 4, onde representámos a
solução
 ).
). 

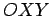 , as rectas
, as rectas  e
e  e ainda as curvas de
nível
e ainda as curvas de
nível  (
( e
e 
 e
e  , digámos
, digámos 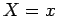 e
e 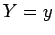 , o valor da
terceira variável
, o valor da
terceira variável  , para o qual o triplo
, para o qual o triplo  , será o
nível
, será o
nível  ).
).  , as rectas
, as rectas  e ainda as curvas de
nível correspondentes a valores constantes de
e ainda as curvas de
nível correspondentes a valores constantes de  tais que
tais que  (
( ).
). 
 ,
correspondente à recta
,
correspondente à recta 
 , isto é,
usámos escalas logarítmicas nos eixos
, isto é,
usámos escalas logarítmicas nos eixos  ,
,  (ver a figura
(ver a figura  )
) 