| O que é a nomografia? |
||
| Next: Um outro exemplo -
Previous: Nomogramas de
cruzamento. Um Índice |
||
|
Em geral, um nomograma de cruzamento para uma equação com três variáveis pode ser construído da seguinte forma:
 Assim, se, relativamente
a um sistema de eixos cartesianos  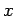 e e 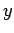 entre estas equações
e a equaçãodada, entre estas equações
e a equaçãodada,
 , para obter a terceira
família de curvas: , para obter a terceira
família de curvas:
 Por
construção, se eliminarmos obtemos a equação
dada
 . Portanto, as curvas
representadas por estas três equações passam por um
mesmo
ponto, exactamente quando os valores correspondentes de . Portanto, as curvas
representadas por estas três equações passam por um
mesmo
ponto, exactamente quando os valores correspondentes de  satisfazem a equação
satisfazem a equação  . . Nos exemplos anteriores
temos, para a primeiro nomograma da equação (1)
(figura 1):  
Next: Um outro exemplo - Previous: Nomogramas de cruzamento. Um Índice Joao Nuno Tavares 2005-03-28 |

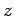 , associámos uma
família de curvas que se intersectam transversalmente, e
indexadas pelos valores de
, associámos uma
família de curvas que se intersectam transversalmente, e
indexadas pelos valores de 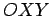 ,
as duas primeiras famílias de curvas são definidas
implicitamente pelas equações:
,
as duas primeiras famílias de curvas são definidas
implicitamente pelas equações: e
e  nas três equações:
nas três equações: 