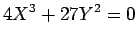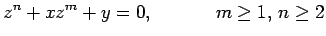| O que é a nomografia? |
||||||
| Next: Nomogramas rectílineos
Previous: Nomogramas
de cruzamento para Índice |
||||||
|
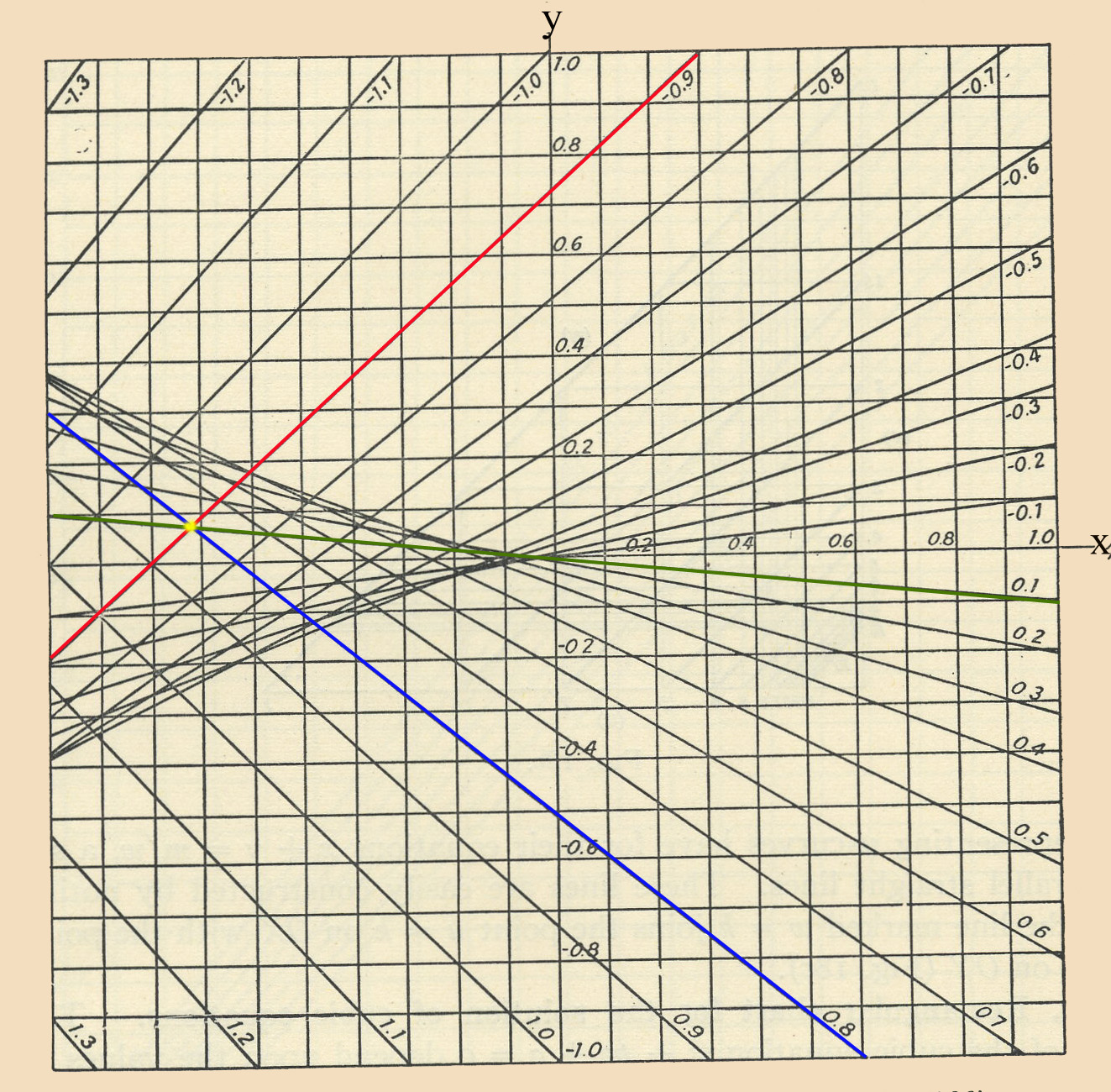
Vejamos um outro exemplo - o nomograma da equação cúbica
O problema consiste em determinar os valores de De acordo com o método geral acima descrito, podemos construir um nomograma pondo:
Relativamente a um sistema de eixos cartesianos
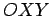 , as duas
primeiras famílias representam as rectas horizontais e
verticais, respectivamente, , as duas
primeiras famílias representam as rectas horizontais e
verticais, respectivamente, 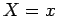 (constante) e (constante) e 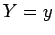 (constante).
Portanto, o ponto do plano de coordenadas (constante).
Portanto, o ponto do plano de coordenadas 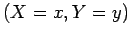 representa a
equação do terceiro grau (5).
A terceira família representa uma família de rectas
(não paralelas) - para cada representa a
equação do terceiro grau (5).
A terceira família representa uma família de rectas
(não paralelas) - para cada 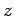 temos a recta de equação temos a recta de equação 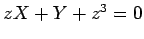 , no plano , no plano 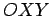 . .
Dada uma equação do terceiro grau (5), com
coeficientes
A família de
rectas 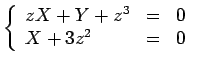 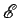 tem equações
paramétricas tem equações
paramétricas
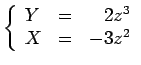
A cúbica envolvente
Existirá uma anamorfose paralela que transforme este nomograma num nomograma rectilíneo paralelo?
Uma discussão análoga permite construir nomogramas para
equações do tipo:
Next: Nomogramas rectílineos Previous: Nomogramas de cruzamento para Índice Joao Nuno Tavares 2005-03-28 |
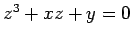
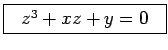
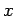 e
e
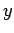 . Portanto, cada par
. Portanto, cada par
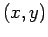 representa uma
equação do
terceiro grau do tipo (
representa uma
equação do
terceiro grau do tipo (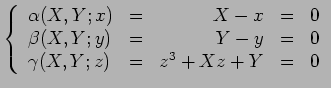
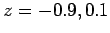 e
e 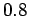 ).
). 
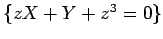 , parametrizada
por
, parametrizada
por