Introdução
|
O cálculo de áreas de polígonos nem
sempre
é uma tarefa
fácil, pela variedade de formas que podem assumir. Não
é
fácil, por exemplo, calcular a área do polígono
seguinte.
 Este polígono é de facto complicado! No entanto, tem a particularidade de ter os seus vértices sobre um reticulado de pontos no plano, constituído por pontos de coordenadas inteiras. Muitas vezes recorremos a processos de dissecção do polígono ou de subtracção de áreas. Todos estes processos envolvem a área como um conceito bidimensional. O novo método que apresentamos permite o cálculo da área pela simples contagem de pontos. |
||
Cálculo da área de polígonos
|
Comecemos por construir um reticulado de pontos de coordenadas inteiras. Daqui
em diante designaremos um
tal reticulado pela letra
|
||
Em situações
simples, a área de um polígono 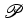 , que
representamos por: , que
representamos por: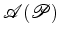 pode ser facilmente
calculada por dissecção, ou
seja,
decompondo-o em triângulos e rectângulos, para os quais
seja
fácil calcular a respectiva área. Eis um exemplo:
|
||
|
Noutras
situações, pode ser mais fácil calcular a
área
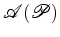 inscrevendo o polígono
num rectângulo. Basta
então calcular a área do rectângulo e subtrair as
áreas dos
polígonos coloridos, como se ilustra no exemplo seguinte:
inscrevendo o polígono
num rectângulo. Basta
então calcular a área do rectângulo e subtrair as
áreas dos
polígonos coloridos, como se ilustra no exemplo seguinte: |
||
Exercício: Calcule a área dos dois polígonos das figuras usando os processos indicados. |
||
| Seguinte:
O Teorema de
Pick e o cálculo de áreas de polígonos Regresso ao Índice |
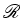 , e
consideraremos apenas
polígonos
, e
consideraremos apenas
polígonos 