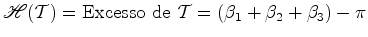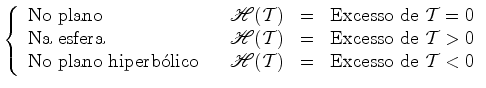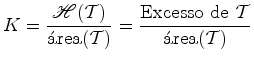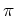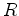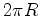| Transporte
paralelo |
|
|
|
Façamos
o
transporte paralelo de um vector tangente ao
longo de
um (pequeno) triângulo geodésico 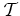 .
Isto significa que o
vector, durante o seu movimento, faz sempre um ângulo constante
com cada um dos três lados desse triângulo. O movimento
faz-se no sentido positivo (anti-horário). .
Isto significa que o
vector, durante o seu movimento, faz sempre um ângulo constante
com cada um dos três lados desse triângulo. O movimento
faz-se no sentido positivo (anti-horário).
Nas três
animações seguintes,
mostra-se o
transporte paralelo em três situações:
|
|
|
|
|
Holonomia
|
|
|
|
A
Holonomia 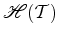 do
triângulo geodésico do
triângulo geodésico 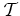 define-se como sendo o menor ângulo
orientado formado pela posição inicial do vector com a
sua
posição final, depois de completado um percurso completo
ao longo
do perímetro de
define-se como sendo o menor ângulo
orientado formado pela posição inicial do vector com a
sua
posição final, depois de completado um percurso completo
ao longo
do perímetro de 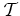 .
.
É possível mostrar que (Gauss-Bonnet):
|
|
Curvatura
de Gauss
|
|
|

|
A curvatura de Gauss 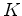 , em cada um destes modelos (de curvatura
constante) pode ser definida por:
, em cada um destes modelos (de curvatura
constante) pode ser definida por:
Não depende do triângulo geodésico.
Portanto:
|
|
Mais
efeitos da curvatura
|
|
|
|
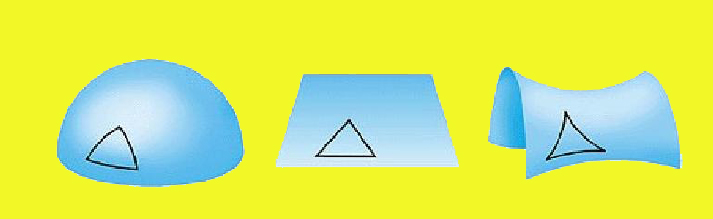
Plano
|
Esfera
|
Curvatura
negativa
|
|
|
|
Rectas perpendiculares
a uma mesma
recta
são paralelas |
Geodésicas perpendiculares
a uma mesma
linha
convergem |
Geodésicas perpendiculares
a uma mesma
linha
divergem |
A
soma
dos ângulos internos
de um triângulo geodésico
é igual a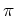 |
A
soma
dos ângulos internos
de um triângulo geodésico
é superior a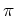 |
A
soma
dos ângulos internos
de um triângulo geodésico
é inferior a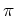 |
O
perímetro de um
círculo
de raio 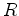
é
igual a 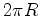
|
O
perímetro de um
círculo
de raio 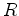
é
inferior a 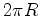 |
O
perímetro de um
círculo
de raio 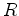
é
superior a 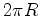 |
Curvatura
K=0
|
Curvatura
K=+1 |
Curvatura
K<0 |
|
|
|
|
|
|
Anterior: O disco rotativo
Próximo: Porquê
espaços-tempo curvos? Gravidade como curvatura do
espaço-tempo
Regresso ao Índice
|
|
|
|
|