Porquê espaços-tempo curvos?
Gravidade como curvatura
do espaço-tempo
|
Variando a aceleração de um observador num espaço-tempo plano, podemos, de acordo com o Princípio de Equivalência, imitar um qualquer campo gravitacional. Então porque necessitamos de espaços-tempo curvos ? Quando discutimos o Princípio de Equivalência, suposemos que o campo gravitacional era uniforme, isto é, que relativamente a um observador de inércia, a aceleração de todos os corpos que caiem é sempre a mesma (em direcção e grandeza). No entanto isto não corresponde à realidade - é só uma aproximação. De facto, a aceleração devida à gravidade varia de ponto para ponto. |
||||||
| Efeitos não locais |
||||||
|
Consideremos as seguintes situações não locais:
Agora, o observador pode
distinguir o campo uniforme da
situação S1. do campo gravitacional terrestre
não uniforme da situação S3..
Novamente, em queda livre, os corpos viajam em geodésicas que
convergem (ou divergem) como na situação S4.
|
||||||
| Efeitos maré |
||||||
|
Estes novos efeitos, chamados "efeitos maré" (tidal effects) da gravidade são provocados pela não uniformidade do campo gravitacional, que varia de ponto para ponto. São, de facto, muito ténues quando analisados localmente. Por outras palavras, uma cápsula muito pequena em queda livre, num intervalo de tempo muito curto, é, em primeira aproximação, um referencial de inércia. Este referencial diz-se por isso um referencial local de inércia. Na presença de um campo gravitacional, por exemplo, na presença de uma massa grande (Terra, Sol, ...), duas partículas teste que se movem com a mesma velocidade inicial ao longo de duas trajectórias espaciais próximas, em geral não continuam paralelas, mas aceleram gradualmente uma relativamente à outra, devido à não uniformidade do campo gravitacional. Esta
aceleração
relativa de partículas em queda
livre é completamente análoga à
situação seguinte. Imaginemos dois viajantes que partem
de dois pontos próximos As trajectórias dos dois viajantes são inicialmente paralelas, mas aproximam-se gradualmente uma da outra até se encontrarem no pólo norte. |
||||||
| Equação do desvio geodésico | ||||||
|
Seja
onde 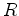 é o
raio da esfera. De facto, tem-se
que: é o
raio da esfera. De facto, tem-se
que:
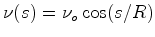
Como que se diz a equação
de Jacobi (ou
equação do
desvio geodésico). De facto esta equação é
válida para
qualquer superfície, desde que definamos apropriadamente
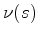 e onde a curvatura pode variar de ponto para ponto
e onde a curvatura pode variar de ponto para ponto 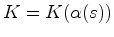 .
.Numa superfície de
curvatura negativa, por exemplo,
geodésicas
inicialmente paralelas afastam-se uma da outra:
|
||||||
| Gravidade como curvatura do espaço-tempo |
||||||
|
A analogia entre as duas situações referidas:
é mais do que uma pura coincidência.
Partindo do seu
Princípio de Equivalência,
Einstein
concluiu que gravidade não é uma força,
como Newton julgava, mas sim curvatura do espaço-tempo. A fonte
desta curvatura é
matéria - um corpo material cria um campo gravitacional que
deforma ou "curva" o espaço-tempo envolvente.
|
||||||
|
Generalizando a lei de
inércia de Newton, que diz
que
partículas livres
deslocam-se segundo geodésicas (linhas rectas) no
espaço-tempo plano da Relatividade Restrita
(gravidade zero = curvatura nula), Einstein afirma que
partículas livres devem seguir geodésicas no
espaço-tempo com curvatura. Portanto, todos os objectos
materais, desde uma maçã até um planeta, movem-se
ao longo de geodésicas do espaço-tempo, a menos que sejam
impedidas por qualquer força exterior. O mesmo acontece com os
raios de luz. Consideremos o movimento de
um planeta (a Terra, por
exemplo)
em
volta do Sol. Duas explicações em confronto:
Vemos pois que, ao considerar o movimento dos corpos no espaço, e ao usar o tempo como uma entidade absoluta e independente, Newton teve que introduzir uma força para explicar o comportamento de uma massa teste junto de uma outra. Einstein não precisa de introduzir uma força para explicar isso. A explicação é puramente geométrica! |
||||||
|
|
||||||
| Próximo: Princípio
da Covariância Geral Anterior: Curvatura Regresso ao Índice |
||||||
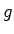 relativamente a um observador de inércia. O
astronauta larga dois corpos, de uma mesma altura, inicialmente em
repouso, e vê esses corpos caiem no chão com
aceleração
relativamente a um observador de inércia. O
astronauta larga dois corpos, de uma mesma altura, inicialmente em
repouso, e vê esses corpos caiem no chão com
aceleração 


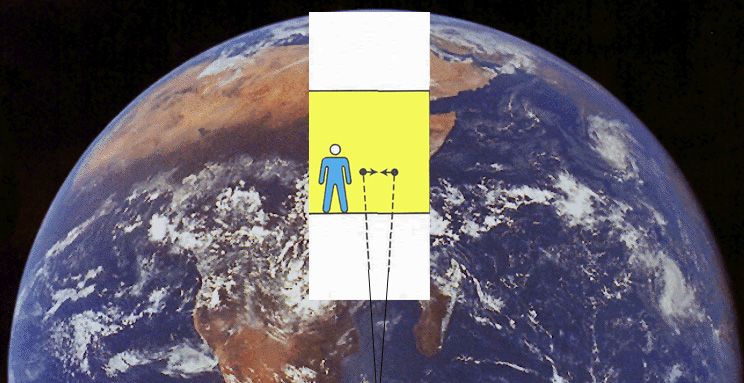
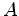 e
e 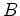 no equador da
esfera, ambos em direcção ao
pólo norte, ao longo de dois meridianos.
no equador da
esfera, ambos em direcção ao
pólo norte, ao longo de dois meridianos. 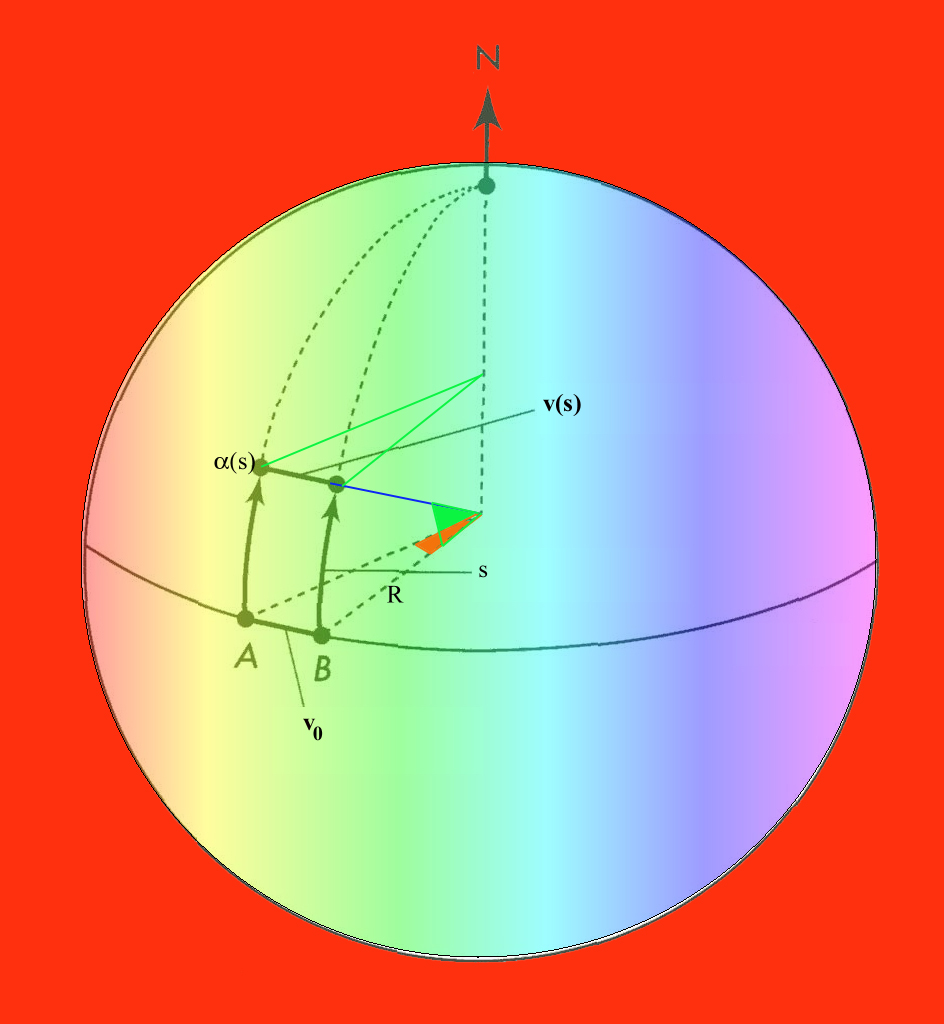
 a
parametrizaçãode um dos meridianos, por comprimento de
arco, com
a
parametrizaçãode um dos meridianos, por comprimento de
arco, com 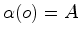 , e seja
, e seja 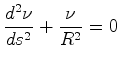
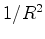 é a curvatura de Gauss da esfera,
podemos escrever:
é a curvatura de Gauss da esfera,
podemos escrever: