|
|
|
|
Um observador que vê um objecto mover-se segundo
uma
trajectória
curvílinea (não rectilínea) dirá que isso
acontece porque,
de acordo com a lei de Newton, existe uma força que actua sobre
esse objecto.
Suponhamos, no entanto, que um outro observador olha para
o
mesmo
objecto e vê que este se desloca segundo uma trajectória
rectilínea, com velocidade uniforme, e que, portanto, novamente
de
acordo com a lei de Newton, não está sujeito à
acção de
qualquer força.
Será isto possível? E quem tem
razão?
Será possível
que dois observadores distintos possam discordar àcerca
(i). da
trajectória ser rectilínea ou curvílinea e
(ii).
àcerca do
facto do objecto estar ou não sujeito à
acção de uma força
exterior?
Vejamos um exemplo concreto:
|
|
Exemplo
|
|
|
|
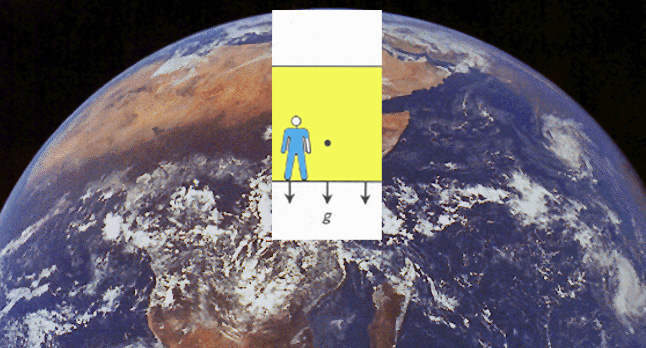
Suponhamos
que um astronauta  está
numa cápsula espacial,
várias dezenas de kms acima da superfície terrestre, em
queda
livre. Um observador está
numa cápsula espacial,
várias dezenas de kms acima da superfície terrestre, em
queda
livre. Um observador  está em
terra e vê o
comportamento
de está em
terra e vê o
comportamento
de  através
de um telescópio. através
de um telescópio.
Figura:
Um astronauta numa cápsula
espacial,
várias dezenas de kms acima
da superfície terrestre, em queda livre.
 |
 está em
repouso na superfície da
terra, e vê está em
repouso na superfície da
terra, e vê  cair
verticalmente
com uma aceleração de cair
verticalmente
com uma aceleração de 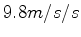 . Tudo o que está na cápsula
espacial comporta-se da mesma forma - tudo cai com a mesma
aceleração. Se, por exemplo,
. Tudo o que está na cápsula
espacial comporta-se da mesma forma - tudo cai com a mesma
aceleração. Se, por exemplo,  atira uma bola
para o lado, atira uma bola
para o lado,  verá a
bola descrever uma parábola, como acontece com
qualquer projéctil. verá a
bola descrever uma parábola, como acontece com
qualquer projéctil.
Consideremos
agora as sensações do astronauta  . Se ele
quiser pôr um quadro na parede da cápsula, basta
encostá-lo,
não precisa de o pregar!
. Se ele
quiser pôr um quadro na parede da cápsula, basta
encostá-lo,
não precisa de o pregar!  compreende que assim é, porque
ele vê que a parede e o quadro caiem ambos com a mesma
aceleração.
compreende que assim é, porque
ele vê que a parede e o quadro caiem ambos com a mesma
aceleração.  larga uma maçã que tem na
mão e vê
que ela permanece suspensa no ar.
larga uma maçã que tem na
mão e vê
que ela permanece suspensa no ar.  dirá que
dirá que  e a maçã caiem lado a lado.
Quando
e a maçã caiem lado a lado.
Quando  atira uma bola, ele verá a
bola deslocar-se em linha recta até colidir com a parede da
cápsula, embora
atira uma bola, ele verá a
bola deslocar-se em linha recta até colidir com a parede da
cápsula, embora  veja a bola
descrever uma parábola. veja a bola
descrever uma parábola.  pesa-se numa
balança a bordo e vê que o seu
peso é
zero! pesa-se numa
balança a bordo e vê que o seu
peso é
zero!
Todas estas experiências
convencem o astronauta  de
que ele está em repouso, num espaço livre de qualquer
atracção gravitacional, enquanto que
de
que ele está em repouso, num espaço livre de qualquer
atracção gravitacional, enquanto que  continua convencido
que
continua convencido
que  cai num campo
de forças uniforme. cai num campo
de forças uniforme.
Para reconciliar estes dois pontos de
vista,  escolhe um
referencial ligado à cápsula, enquanto que
escolhe um
referencial ligado à cápsula, enquanto que  escolhe um
referencial
ligado à terra. Estes dois referenciais movem-se um
relativamente ao
outro com aceleração linear constante. As
consequências
imediatas deste facto são escolhe um
referencial
ligado à terra. Estes dois referenciais movem-se um
relativamente ao
outro com aceleração linear constante. As
consequências
imediatas deste facto são
(i).
aquilo a que  chama uma
recta,
chama uma
recta,  dirá que é uma curva,
dirá que é uma curva,
(ii). uma região que  declara que está livre de qualquer
atracção
gravitacional,
declara que está livre de qualquer
atracção
gravitacional,  dirá que está sujeita a um campo
gravitacional uniforme.
dirá que está sujeita a um campo
gravitacional uniforme.
Esta
relação
é
recíproca -  dirá que a terra e
dirá que a terra e  se deslocam
com aceleração
uniforme na
sua direcção. se deslocam
com aceleração
uniforme na
sua direcção.
Como
vimos, a teoria da
Relatividade Geral proíbe que
privilegiemos qualquer observador relativamente a qualquer outro.
Não
pode haver qualquer tipo de favoritismo. Qualquer lei da Natureza
é igualmente aceitável para todos os observadores e deve
por isso ter
uma forma invariante que sobreviva à mudança de
coordenadas
correspondentes. Em particular, a situação acima descrita
mostra
que a força gravitacional é uma ilusão - depende
do referencial
escolhido. Isto não significa que se nos lançarmos do
cimo de
uma torre não haja consequências desastrosas! Mas Einstein
nega
que elas se devem à atracção que a terra exerce
sobre nós!
Veremos em breve qual a explicação de Einstein.
No exemplo acima, consideramos o efeito da
gravitação apenas
numa pequena região que, de acordo com Newton, está
sujeita à
acção de um campo uniforme. Vimos que, nesta
situação, todos os
seus efeitos podem ser neutralizados por uma mudança de
referencial. A existência de um campo gravitacional uniforme, de
acordo
com  , é negada pelo astronauta
, é negada pelo astronauta  que escolhe um
referencial
que se move com aceleração constante relativamente a que escolhe um
referencial
que se move com aceleração constante relativamente a  . Um
outro observador ligado ao seu referencial afirmará porventura a
existência
de um outro tipo de campo.
. Um
outro observador ligado ao seu referencial afirmará porventura a
existência
de um outro tipo de campo.
Uma escolha conveniente de
referencial neutralizará qualquer
campo
gravitacional uniforme. Portanto, um campo deste tipo é
artificial, uma pura invenção do observador, e não
uma propriedade
intrínseca da Natureza...
Einstein resumiu estas
conclusões no seu Princípio da Equivalência que,
numa primeira formulação, pode ser enunciado na forma
seguinte:
|
|
|
|
Princípio da
Equivalência [Einstein] ...
A Física num referencial em queda livre num campo
gravitacional uniforme é equivalente à Física num
referencial de inércia sem gravidade.
Por outras palavras, dentro de um referencial em queda livre, onde a
aceleração cancela exactamente o campo gravitacional
uniforme, não é
possível detectar nem a aceleração nem a
gravidade através
de qualquer experiência.
|
|
|
|
Portanto,
de acordo com o Princípio de Equivalência,
referenciais acelerados podem ser tratados
da mesma forma que os referenciais de inércia - eles
não
são mais do que referenciais de inércia
com gravidade. Daqui resulta também uma definição
física de
referencial de inércia, sem qualquer referência a algo de
exterior como, por
exemplo, estrelas fixas - um referencial de inércia é
apenas um referencial sem
gravidade.
|
|
Mais
exemplos
|
|
|
|
Consideremos
as seguintes
situações locais:
- S 1
- ... Uma caixa é colocada
num foguetão longe da acção de qualquer campo
gravitacional. O foguetão é
acelerado para a frente com aceleração constante
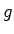 relativamente a um observador de inércia. O observador dentro da
caixa larga um corpo inicialmente em repouso e vê esse corpo cair
no chão com aceleração
relativamente a um observador de inércia. O observador dentro da
caixa larga um corpo inicialmente em repouso e vê esse corpo cair
no chão com aceleração 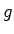 . .
Figura: Uma caixa é colocada
num foguetão longe da acção de qualquer campo
gravitacional. O foguetão é
acelerado para a frente com aceleração constante 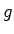 relativamente a um observador de inércia. O observador dentro da
caixa larga um corpo inicialmente em repouso e vê esse corpo cair
no chão com aceleração
relativamente a um observador de inércia. O observador dentro da
caixa larga um corpo inicialmente em repouso e vê esse corpo cair
no chão com aceleração 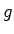 .
.
 |
- S 2
- Desligam-se os motores do foguetão
de tal forma que
agora
a caixa desloca-se com movimento uniforme relativamente ao observador
de inércia anterior. O observador dentro da caixa larga um corpo
e vê esse corpo flutuar, permanecendo em repouso relativamente ao
observador.
Figura:
Desligam-se os motores
do foguetão de tal forma que agora a caixa desloca-se com
movimento uniforme relativamente ao observador de inércia
anterior. O observador dentro da caixa larga um corpo e vê esse
corpo flutuar, permanecendo em repouso relativamente ao observador.
 |
- S 3
- ... A caixa é colocada na
superfície da
Terra.
Ignoram-se os movimentos de rotação e orbital da Terra. O
observador dentro da caixa larga um corpo inicialmente em repouso e
vê esse corpo cair no chão com aceleração
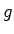 . .
Figura:
A caixa é colocada
na superfície da Terra. Ignoram-se os movimentos de
rotação e orbital da Terra. O observador dentro da caixa
larga um corpo inicialmente em repouso e vê esse corpo cair no
chão com aceleração 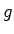 .
.
 |
- S 4
- ... A caixa é colocada num
poço terrestre e
cai
livremente em direcção ao centro da Terra. O astronauta
dentro da caixa larga um corpo e vê esse corpo flutuar,
permanecendo em repouso relativamente a ele próprio.
Figura:
A caixa é colocada
num poço terrestre e cai livremente em direcção ao
centro da Terra. O astronauta dentro da caixa larga um corpo e vê
esse corpo flutuar, permanecendo em repouso relativamente a ele
próprio.
 |
Claramente que, do ponto de vista do astronauta, dentro
da
caixa, as
situações S 1 e S 3 são
indistinguíveis, bem
como as situações S 2 e S 4, de acordo
com o Princípio de Equivalência que, numa segunda
formulação, enunciamos na forma seguinte:
|
|
|
|
Princípio da
Equivalência [Einstein] ...
"Se nos
restringirmos a uma pequena região do espaço, um campo de
gravitação uniforme é equivalente a um referencial
que se move com
aceleração linear constante, num campo livre de
gravidade.
Não é
possível distinguir as duas situações por qualquer
experiência" .
Por outras palavras,
um
campo de
gravitação é localmente equivalente a um campo de
aceleração.
Um referencial acelerado e um campo de gravitação, que
aponta na
direcção contrária à da
aceleração, são equivalentes.
Não existe maneira de distinguir as duas
situações!
|
|
|
Outro
exemplo:
|
|
|
|
Eis
um exemplo ilustrativo do
Princípio da Equivalência, na situação
simples em que temos
dois referenciais, 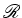 e
e 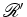 , cuja aceleração relativa é
constante em grandeza e direcção.
, cuja aceleração relativa é
constante em grandeza e direcção.
Consideremos um
sistema de partículas com massas 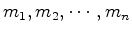 ,
interagindo umas com as outras de tal forma
que cada uma delas exerce uma força sobre cada uma das
restantes. ,
interagindo umas com as outras de tal forma
que cada uma delas exerce uma força sobre cada uma das
restantes.
Para 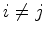 , seja
, seja 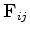 a força que a partícula
a força que a partícula 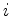 exerce sobre a partícula
exerce sobre a partícula 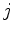 . Por simplicidade, supômos que
. Por simplicidade, supômos que
(i).
a força está dirigida segundo a linha que une as
partículas 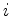 e e 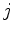 ,
,
(ii). é uma função apenas da distância
entre elas,
e
(iii). 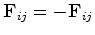 ,
, 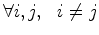 .
.
Um
observador  ligado ao
referencial ligado ao
referencial 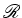 usa
coordenadas usa
coordenadas 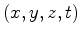 para acontecimentos, enquanto que um
observador
para acontecimentos, enquanto que um
observador  , ligado ao
referencial
, ligado ao
referencial 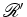 , usa coordenadas
, usa coordenadas 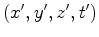 para esses mesmos
acontecimentos. Supômos ainda que as velocidades envolvidas
são
suficientemente pequenas para que seja possível uma
análise
não relativista. Pômos portanto
para esses mesmos
acontecimentos. Supômos ainda que as velocidades envolvidas
são
suficientemente pequenas para que seja possível uma
análise
não relativista. Pômos portanto 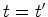 e
usamos a notação:
e
usamos a notação:
Sejam
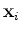 e e
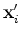 ,
os vectores de posição da partícula ,
os vectores de posição da partícula 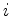 , , 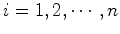 , relativamente aos referenciais
, relativamente aos referenciais 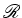 e e 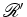 ,
respectivamente.
,
respectivamente.
Se o primeiro
observador  acredita que
está na presença
de um campo gravitacional uniforme, de tal forma que, relativamente
a ele, todas as partículas livres caiem com a mesma
aceleração,
dada por um vector constante acredita que
está na presença
de um campo gravitacional uniforme, de tal forma que, relativamente
a ele, todas as partículas livres caiem com a mesma
aceleração,
dada por um vector constante 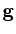 , então as equações do
movimento são, para esse observador:
, então as equações do
movimento são, para esse observador:
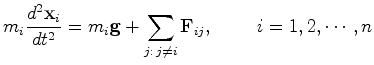 |
(8) |
já que, de acordo com a segunda
lei de Newton:
Suponhamos
que a aceleração relativa entre
os dois
referenciais, 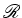 e
e 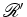 , é constante em grandeza e direcção. Mais
concretamente:
, é constante em grandeza e direcção. Mais
concretamente:
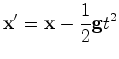 |
(9) |
Derivando duas vezes, obtem-se:
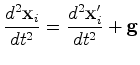 |
(10) |
Substituindo,
para cada 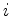 , a equação (10)
em
(8),
obtemos as seguintes equações do
movimento,
descritas agora no referencial
, a equação (10)
em
(8),
obtemos as seguintes equações do
movimento,
descritas agora no referencial 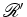 , i.e., relativas ao segundo
observador
, i.e., relativas ao segundo
observador  :
:
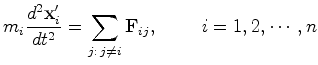 |
(11) |
Nota:
como 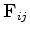 é apenas função de
é apenas função de 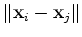 ,
e como ,
e como 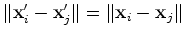 ,
, 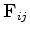 é o mesmo em ambos os referenciais.
é o mesmo em ambos os referenciais.
Conclusão: O campo gravitacional foi
cancelado
no referencial 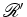 . Para o observador
. Para o observador  não
existe campo
gravitacional. O observador não
existe campo
gravitacional. O observador  interpreta
isto dizendo que interpreta
isto dizendo que  está em queda livre e que por isso não sente campo
gravitacional. Por outro lado,
está em queda livre e que por isso não sente campo
gravitacional. Por outro lado,  poderá
dizer: "Não, meu
caro! De facto não existe campo gravitacional. Eu sou um
observador
inercial e você sente campo gravitacional apenas pelo facto de
que
você acelera relativamente a mim!" poderá
dizer: "Não, meu
caro! De facto não existe campo gravitacional. Eu sou um
observador
inercial e você sente campo gravitacional apenas pelo facto de
que
você acelera relativamente a mim!"
|
|
|
|
|
|
|
Próximo: Princípio da Equivalência.
Massa de
inércia e massa gravitacional
Anterior: Princípio de Mach
Regresso ao Índice
|
|
|
|
|
 , se move com aceleração constante e igual
a
, se move com aceleração constante e igual
a  , relativamente a um referencial de inércia
, relativamente a um referencial de inércia  .
.
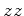 e que os
restantes eixos se mantêm sempre paralelos. A
relação entre as
coordenadas dos dois referenciais é dada por:
e que os
restantes eixos se mantêm sempre paralelos. A
relação entre as
coordenadas dos dois referenciais é dada por: 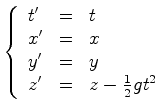
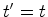 . Consideremos
agora uma partícula livre
(ou um raio de luz)
que se move com velocidade constante
. Consideremos
agora uma partícula livre
(ou um raio de luz)
que se move com velocidade constante 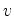 , no plano
, no plano 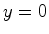 ,
paralelamente ao eixo dos
,
paralelamente ao eixo dos 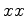 no referencial
de
inércia
no referencial
de
inércia 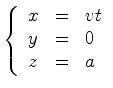
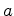 é uma constante.
Portanto:
é uma constante.
Portanto: 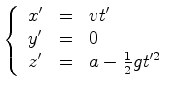
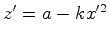 no plano
no plano 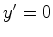 do
referencial
do
referencial 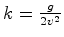 . Portanto, quando obervada no referencial
. Portanto, quando obervada no referencial  está
numa cápsula espacial,
várias dezenas de kms acima da superfície terrestre, em
queda
livre. Um observador
está
numa cápsula espacial,
várias dezenas de kms acima da superfície terrestre, em
queda
livre. Um observador  está em
terra e vê o
comportamento
de
está em
terra e vê o
comportamento
de 
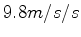 . Tudo o que está na cápsula
espacial comporta-se da mesma forma - tudo cai com a mesma
aceleração. Se, por exemplo,
. Tudo o que está na cápsula
espacial comporta-se da mesma forma - tudo cai com a mesma
aceleração. Se, por exemplo, 



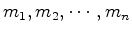 ,
interagindo umas com as outras de tal forma
que cada uma delas exerce uma força sobre cada uma das
restantes.
,
interagindo umas com as outras de tal forma
que cada uma delas exerce uma força sobre cada uma das
restantes.  , seja
, seja 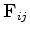 a força que a partícula
a força que a partícula 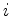 exerce sobre a partícula
exerce sobre a partícula 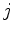 . Por simplicidade, supômos que
. Por simplicidade, supômos que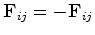 ,
, 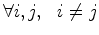 .
. 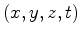 para acontecimentos, enquanto que um
observador
para acontecimentos, enquanto que um
observador 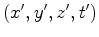 para esses mesmos
acontecimentos. Supômos ainda que as velocidades envolvidas
são
suficientemente pequenas para que seja possível uma
análise
não relativista. Pômos portanto
para esses mesmos
acontecimentos. Supômos ainda que as velocidades envolvidas
são
suficientemente pequenas para que seja possível uma
análise
não relativista. Pômos portanto 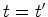 e
usamos a notação:
e
usamos a notação: 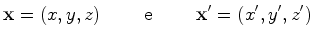
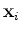 e
e
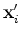 ,
os vectores de posição da partícula
,
os vectores de posição da partícula 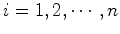 , relativamente aos referenciais
, relativamente aos referenciais 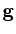 , então as equações do
movimento são, para esse observador:
, então as equações do
movimento são, para esse observador: 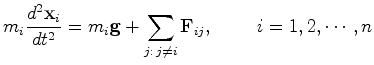
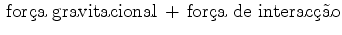
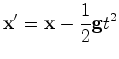
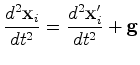
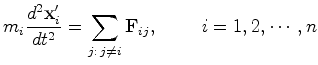
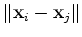 ,
e como
,
e como 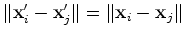 ,
,