Princípio da Equivalência
Massa de inércia e massa gravitacional
| Massa
de inércia |
||||||
|
A massa de inércia, que relaciona a força total, que actua sobre o corpo, com a aceleração resultante. |
||||||
| Massa
gravitacional |
||||||
|
Se o corpo está sob a
acção de um campo
gravitacional,
criado por um outro corpo esférico de massa (gravitacional) onde 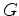 é uma
constante universal: é uma
constante universal: 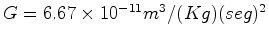 .
.
Portanto, a massa
gravitacional mede a resposta de um
objecto à atracção gravitacional. Podemos ver
estas massas
gravitacionais como fontes que geram força gravitacional, ou
ainda como "cargas" gravitacionais que se atraiem uma à outra.
A massa de
inércia |
||||||
| Princípio da Equivalência de Newton | ||||||
| |
Para comparar estas duas
noções de massa, consideremos
como a
gravidade terrestre actua sobre um corpo situado à
superfície da
terra. Neste caso,
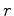 será
igual à
distância entre o corpo e
o centro da terra e será
igual à
distância entre o corpo e
o centro da terra e 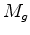 a massa gravitacional da terra.
a massa gravitacional da terra. 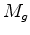 e
e 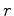 são
pois constantes. A
força gravitacional são
pois constantes. A
força gravitacional 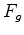 ,
dada por (13),
que actua sobre o corpo, é
portanto
proporcional à sua massa gravitacional
,
dada por (13),
que actua sobre o corpo, é
portanto
proporcional à sua massa gravitacional 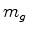 :
:
Mas a segunda lei de Newton (12), diz que essa força é também igual a 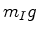 ,
onde ,
onde 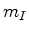 é a massa de inércia
do corpo e
é a massa de inércia
do corpo e 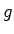 a
aceleração devida à gravidade. Portanto:
a
aceleração devida à gravidade. Portanto:
Se existissem dois corpos
para os quais
Newton postulou que a
razão,
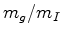 , entre as duas massas
de um mesmo corpo, é independente da substância de que ele
é
feito. Escolhendo convenientemente as unidades podemos até
supôr que:
, entre as duas massas
de um mesmo corpo, é independente da substância de que ele
é
feito. Escolhendo convenientemente as unidades podemos até
supôr que:Este postulado tem o nome de Princípio da Equivalência de Newton. A queda livre de corpos no vazio suporta
experimentalmente
este
postulado - todos os corpos caiem com a mesma aceleração
num
campo gravitacional dado.
|
|||||
| Novamente o Princípio da Equivalência | A lei de atracção universal confere pois à força de atracção gravitacional uma característica única entre todas as forças conhecidas na Natureza. De facto, enquanto que uma
força qualquer
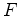 , quando actua
num corpo, comunica-lhe uma
aceleração, , quando actua
num corpo, comunica-lhe uma
aceleração, 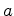 , que depende da sua massa
, que depende da sua massa 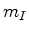 : :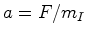 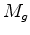 , comunica a esse corpo uma aceleração que
não depende da sua
massa:
, comunica a esse corpo uma aceleração que
não depende da sua
massa: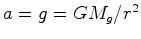
já que A aceleração da gravidade é portanto a mesma para todos os corpos - a força gravitacional ajusta-se de alguma forma à massa de cada corpo sobre o qual actua, de tal forma que a todos imprime a mesma aceleração! É esta aliás a propriedade notável do campo gravitacional, que torna possível criá-lo artificialmente. Corpos em queda livre, isto é, sujeitos apenas à acção da gravidade, caiem lado a lado, todos com a mesma aceleração. Mas, como já vimos na secção anterior, podemos simular exactamente a mesma situação, por exemplo, no interior de uma nave, fora da influência de qualquer campo gravitacional, cujos motores a impulsionam numa direcção fixa com uma aceleração constante. Corpos em queda livre dentro da nave sofrem todos uma mesma aceleração na direcção oposta. Portanto, num referencial ligado à nave, criámos um campo gravitacional. Podemos até
neutralizar um campo gravitacional. Isto
é
o que acontece nos aviões
Mas regressemos ao
Princípio da Equivalência de
Newton: A explicação
de Einstein está mais uma vez no seu: Princípio da Equivalência ... Um campo de gravitação é localmente equivalente a um campo de aceleração. Um referencial acelerado e um campo de gravitação, que aponta na direcção contrária à da aceleração, são equivalentes. Não existe maneira de distinguir as duas situações!
Existem duas explicações possíveis:
Os efeitos de um campo
gravitacional e de um campo de
aceleração são pois os
mesmos e um observador, situado no interior da caixa, não tem
maneira de
distinguir entre as duas situações acima descritas. Em E1.
(campo gravitacional), o
alongamento da mola é determinado pela massa gravitacional É esta a
explicação dada por
Einstein para a
igualdade |
|||||
|
|
||||||
| Próximo: Consequências do
Princípio
da Equivalência Anterior: Princípio da Equivalência. Introdução Regresso ao Índice |
||||||
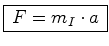
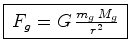
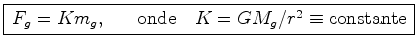
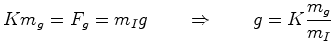

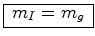
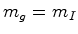 .
. , usados em experiências para testar ausência de peso. De
20 em 20 segundos, eles voam como um projéctil que é
disparado para cima e depois cai sob a acção da gravidade
terrestre. Dentro do avião, objectos que se movem livremente,
caiem exactamente como o avião, à mesma razão.
Portanto, relativamente a um referencial ligado ao avião, eles
exibem aceleração nula. Eles flutuam. A gravidade
terrestre foi cancelada ou neutralizada e atinge-se o ponto
, usados em experiências para testar ausência de peso. De
20 em 20 segundos, eles voam como um projéctil que é
disparado para cima e depois cai sob a acção da gravidade
terrestre. Dentro do avião, objectos que se movem livremente,
caiem exactamente como o avião, à mesma razão.
Portanto, relativamente a um referencial ligado ao avião, eles
exibem aceleração nula. Eles flutuam. A gravidade
terrestre foi cancelada ou neutralizada e atinge-se o ponto 
 .
Como explicar esta igualdade entre massa de inércia
.
Como explicar esta igualdade entre massa de inércia 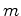 suspenso por
uma
mola, presa à
parte superior de uma caixa (um elevador, por exemplo). Um observador
dentro da caixa vê subitamente a mola alongar-se. O
acréscimo da tensão da mola indica que o corpo foi
puxado.
suspenso por
uma
mola, presa à
parte superior de uma caixa (um elevador, por exemplo). Um observador
dentro da caixa vê subitamente a mola alongar-se. O
acréscimo da tensão da mola indica que o corpo foi
puxado. 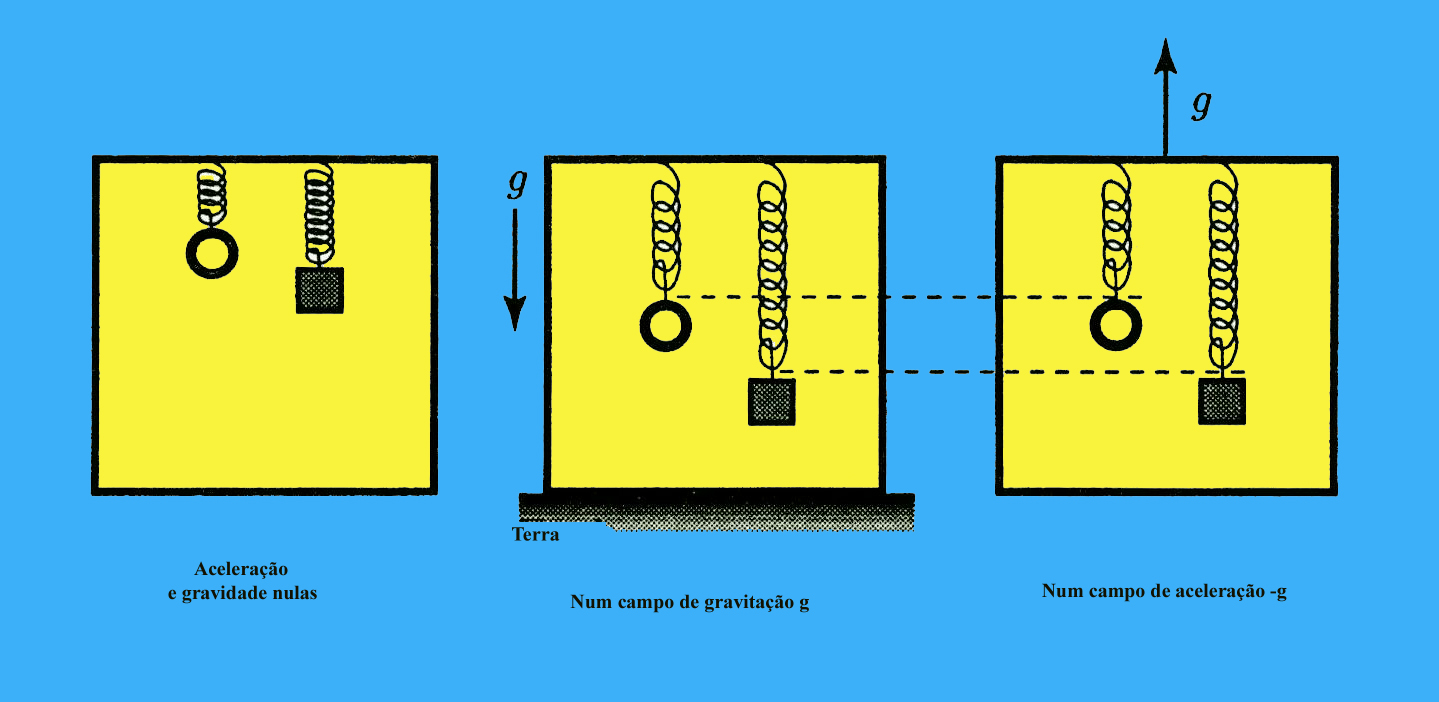
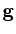 , e a mola sofre um alongamento
, e a mola sofre um alongamento 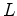 .
. 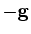 .
A mola sofre um alongamento idêntico
.
A mola sofre um alongamento idêntico