Consequências do
Princípio de Equivalência
| Em 1911
Einstein deduziu
várias consequências do seu
Princípio de Equivalência. |
|||||
"Redshift"gravitacional |
|||||
|
Considere a seguinte
experiência conceptual: luz de
frequência A luz é detectada por
um
receptor, estacionado no topo da
nave. Que frequência é que ele mede ?
Note que o receptor não é um observador de inércia. Como podemos pois dizer algo àcerca das suas medições? Einstein assumiu a hipótese, válida em primeira aproximação para acelerações fracas, que toda a medição feita por um observador acelerado é a mesma da que é obtida por um observador de inércia, que tem a mesma velocidade no instante e local em que é feita a medição. Sendo
assim, seja É claro que emissor e
receptor afastam-se um do outro.
Portanto,
de acordo com a teoria do efeito
Doppler, a frequência
aproximação válida para baixas velocidades 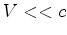 . Em primeira
aproximação, o tempo
. Em primeira
aproximação, o tempo 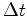 que a luz demora a percorrer a
distância
que a luz demora a percorrer a
distância 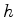 , é igual a:
, é igual a:
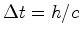
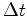 , muito pequeno, o topo
do elevador aumentou a sua velocidade de:
, muito pequeno, o topo
do elevador aumentou a sua velocidade de: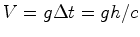 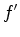 medida pelo receptor é:
medida pelo receptor é:
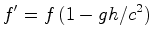
De acordo com o
Princípio
de Equivalência, o mesmo
efeito deve ser observado se o
elevador, em vez de estar acelerado, está sob a
acção de um
campo gravitacional dirigido para baixo. Como o receptor está,
neste caso, sempre em repouso relativamente ao emissor, ele não
pode atribuir o reshift ao efeito Doppler. Deve sim
interpretá-lo
como um efeito da gravidade. Concluímos pois:
|
|||||
Dilatação gravitacional do tempo |
|||||
|
Vamos comparar dois relógios
Figura
11
Para ver isto, imaginemos
que o
relógio No instante 0
, o relógio No segundo seguinte, É claro que Portanto, os dois pulsos que
foram emitidos por Por outras palavras, o
astronauta
na base do foguetão
concluirá que o relógio Se o astronauta estivesse no
nariz do foguetão, observando
agora, junto de |
|||||
|
Pelo Princípio de
Equivalência, o mesmo se passa quando
o foguetão está estacionado à superfície da
Terra, sujeito pois ao campo gravitacional terrestre.
Como neste caso,
Este fenómeno da
dilatação gravitacional do
tempo complica a
atribuição de coordenadas temporais a acontecimentos, na
presença de um
campo gravitacional. De facto, em Relatividade Restrita, a coordenada
temporal de um acontecimento, num dado
referencial de inércia, define-se pela leitura de um
relógio em repouso,
relativamente a esse referencial, e situado no mesmo local desse
acontecimento. Como
temos a possibilidade de sincronizar todos os relógios num dado
referencial de inércia, este processo atribui de forma
unívoca um valor para a
coordenada temporal de cada acontecimento.
Mas, num campo gravitacional, os relógios em diferentes locais marcam o tempo de forma diferente, i.e., os tics dos relógios são diferentes conforme o local onde eles se encontram. Portanto eles não podem ser sincronizados. Como podemos então comparar as coordenadas temporais de acontecimentos que ocorrem em locais distintos ? Suponhamos que se pretende
fazer
um rectângulo no
espaço-tempo. Começamos por usar um diagrama "altura Tomemos agora um segundo
objecto
que está mais alto
Para agravar esta situação, veremos em breve que a própria geometria é ela própria alterada pela presença de um campo gravitacional (veja a discussão sobre o disco rotativo)! Como podemos então definir coordenadas espaciais para acontecimentos no espaço-tempo?
|
|||||
 |
A resposta é Geometria Riemanniana (1826-1866). | ||||
Deflexão da luz num campo gravitacional |
|||||
|
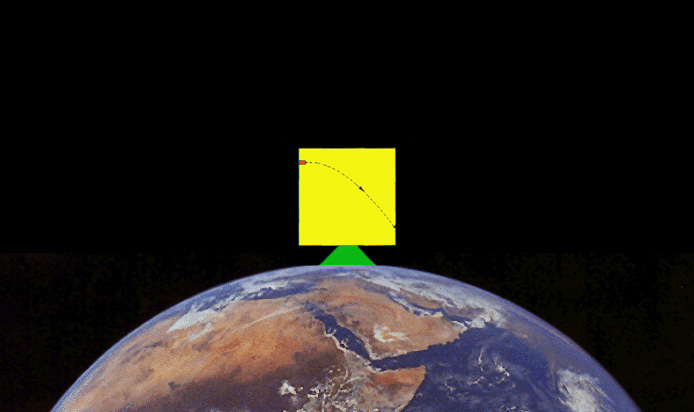
Considere a seguinte
experiência conceptual: um pulso de luz
é
emitido de um ponto
Figura
13
(applett construído com Flash por Vanessa Oliveira) No instante em que a luz atinge a outra parede mais
afastada, o
elevador subiu uma certa distância. A luz atinge essa parede num
certo ponto Um astronauta dentro da nave observa pois que o pulso de luz descreve uma trajectória parabólica.
Pelo Princípio de Equivalência, o mesmo será observado pelo astronauta quando a nave não acelera mas está em repouso à superfície da Terra.
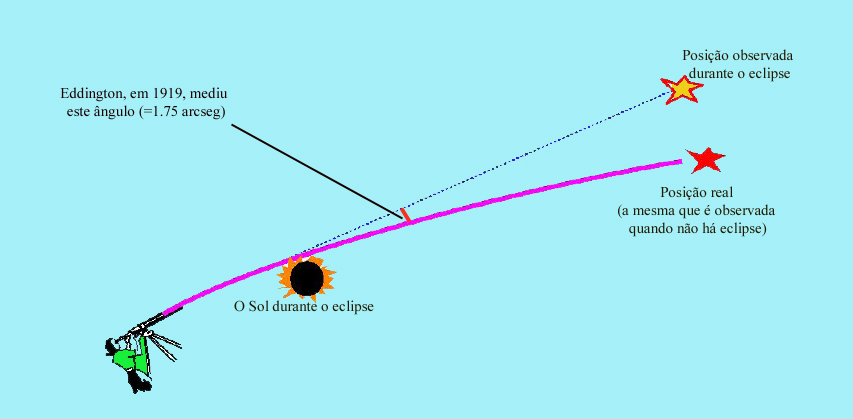
Ver o teste real da deflexão da luz solar, durante o eclipse de 1919.
|
|||||
|
|
|||||
| Próximo: O disco rotativo Anterior: Princípio da equivalência (massa de inércia e massa gravitacional) Regresso ao Índice |
|||||
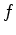 é emitida do chão de uma nave de altura
é emitida do chão de uma nave de altura 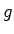 , dirigida para cima, no
espaço exterior, longe de qualquer campo gravitacional.
, dirigida para cima, no
espaço exterior, longe de qualquer campo gravitacional. um referencial
de inércia no qual o
emissor está
momentâneamente em repouso, no instante em que emite o raio
luminoso, e
um referencial
de inércia no qual o
emissor está
momentâneamente em repouso, no instante em que emite o raio
luminoso, e  um referencial
de inércia no qual o receptor
está em repouso
quando a luz é detectada.
um referencial
de inércia no qual o receptor
está em repouso
quando a luz é detectada. 
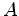 e
e 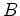 , o primeiro colocado no
topo e o segundo na base de um foguetão, quando este acelera
para cima (figura
, o primeiro colocado no
topo e o segundo na base de um foguetão, quando este acelera
para cima (figura 
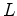 , atinge
, atinge 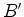 (figura
(figura 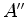 emite o
próximo pulso em direcção a
emite o
próximo pulso em direcção a 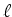 ,
atinge
,
atinge 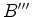 (figura
(figura 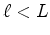 , uma vez que o foguetão acelera e tem por
isso mais velocidade no instante da emissão do segundo pulso.
, uma vez que o foguetão acelera e tem por
isso mais velocidade no instante da emissão do segundo pulso. 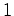 segundo,
chegam a
segundo,
chegam a 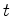 ". Como base
do nosso rectângulo tomamos um objecto
". Como base
do nosso rectângulo tomamos um objecto 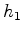 , e seguimos a sua linha de universo durante
, e seguimos a sua linha de universo durante 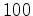 segundos. Obtemos assim uma linha
segundos. Obtemos assim uma linha 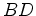 paralela ao
eixo dos
paralela ao
eixo dos 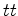 (figura
(figura 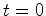 . Começando em
. Começando em 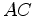 . No entanto
como o tempo anda diferentemente às duas altitudes, os dois
pontos
. No entanto
como o tempo anda diferentemente às duas altitudes, os dois
pontos 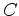 e
e 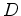 não
são
simultâneos. Portanto o espaço-tempo é curvo
(figura
não
são
simultâneos. Portanto o espaço-tempo é curvo
(figura 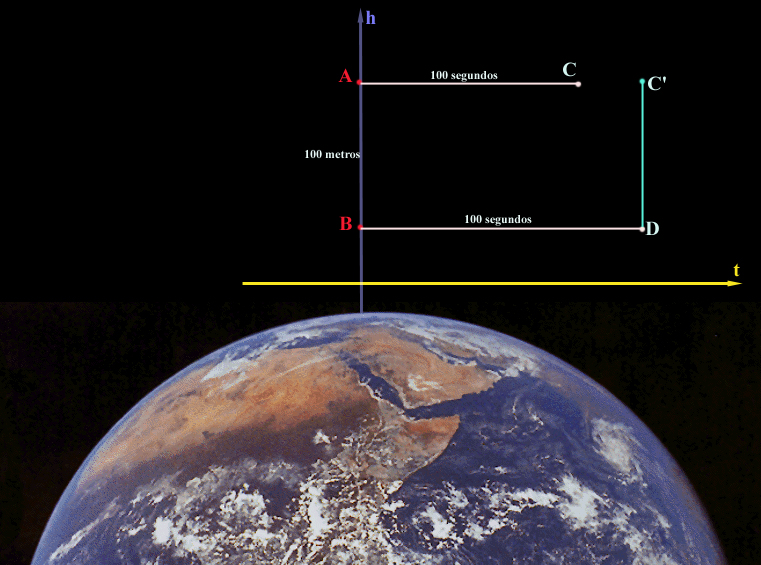
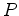 , numa direcção perpendicular ao movimento
de uma nave, que se move com uma aceleração linear
constante
, numa direcção perpendicular ao movimento
de uma nave, que se move com uma aceleração linear
constante 
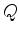 , que está mais abaixo do que o ponto
, que está mais abaixo do que o ponto