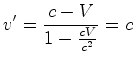|
Seja 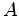 um acontecimento e suponhamos que: um acontecimento e suponhamos que:
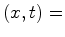 coordenadas de coordenadas de 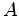 relativamente a um referencial relativamente a um referencial  .
. 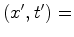 coordenadas de coordenadas de 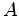 relativamente a um referencial relativamente a um referencial  , em movimento uniforme com velocidade
, em movimento uniforme com velocidade 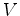 , relativamente a
, relativamente a  .
.
A figura torna claro que (justifique):
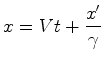 |
(39) |
ou:
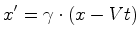 |
(40) |
Anàlogamente, se deduz que:
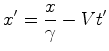 |
(41) |
ou:
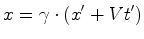 |
(42) |
Eliminando 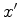 nas
equações (40) e (42),
obtem-se: nas
equações (40) e (42),
obtem-se:
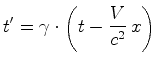 |
(43) |
enquanto que eliminando 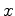 nas mesmas equações
se obtem: nas mesmas equações
se obtem:
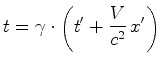 |
(44) |
Estas duas últimas equações
substituem a equação simples 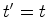 da relatividade de Galileu
(tempo absoluto). da relatividade de Galileu
(tempo absoluto).
|
|
|
 |
(45) |
Em
muitas situações o mais importante é o intervalo
de tempo
entre dois acontecimentos 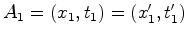 e e 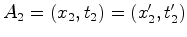 . Usando as fórmulas
anteriores, obtemos:
. Usando as fórmulas
anteriores, obtemos:
onde pusemos:
Anàlogamente:
Um
cálculo simples mostra que:
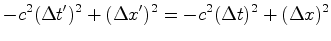 |
(48) |
donde se deduz
que:
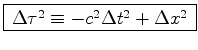 |
(49) |
(onde pusemos 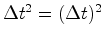 ,
etc...) é um invariante das
transformações de Lorentz, a que se
chama a separação (espaço-temporal) entre os dois
acontecimentos
,
etc...) é um invariante das
transformações de Lorentz, a que se
chama a separação (espaço-temporal) entre os dois
acontecimentos 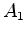 e e 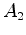 .
. |
|
|
- Relatividade
da simultaneidade ... Acontecimentos
espacialmente separados e que são simultâneos num certo
referencial
 , nunca são simultâneos quando descritos num outro
referencial
, nunca são simultâneos quando descritos num outro
referencial  que se move com
velocidade constante que se move com
velocidade constante 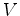 relativamente ao
primeiro. relativamente ao
primeiro.
Dados: 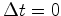 e e 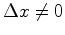 .
.
Portanto:
donde:
O
segundo membro é zero sse 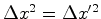 o que só
pode ocorrer quando o que só
pode ocorrer quando 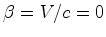 .
.
Por outro lado, por (46):
- Dilatação
do tempo ... Se dois acontecimentos ocorrem no mesmo
local, relativamente a um referencial
 , a sua separação temporal,
medida por observadores ligados a esse referencial (intervalo de tempo
próprio)
, a sua separação temporal,
medida por observadores ligados a esse referencial (intervalo de tempo
próprio)  ,
é menor do que a separação temporal entre
esses mesmos
acontecimentos, medida por observadores ligados a um outro referencial
,
é menor do que a separação temporal entre
esses mesmos
acontecimentos, medida por observadores ligados a um outro referencial  que
se move com velocidade constante que
se move com velocidade constante 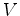 relativamente ao primeiro. relativamente ao primeiro.
Dados: 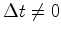 e e 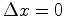 .
.
Portanto:
donde:
Por outro lado, por (47):
como já tínhamos visto
(contracção do comprimento).
- Fórmula da adição de
velocidades ...
Consideremos uma
partícula que se desloca com velocidade constante 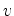 , medida relativamente a um referencial
, medida relativamente a um referencial  , com equação de movimento:
, com equação de movimento:
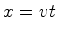 |
(50) |
Transformando esta
equação nas coordenadas 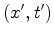 , relativas a um outro referencial
, relativas a um outro referencial  que se move com velocidade constante que se move com velocidade constante
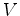 relativamente ao primeiro, usando (40) e
rearranjando termos,
obtem-se:
relativamente ao primeiro, usando (40) e
rearranjando termos,
obtem-se:
-
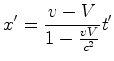 |
(51) |
que descreve
novamente um movimento com velocidade constante 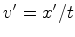 dada por: dada por:
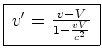 |
(52) |
No limite não relativista, com ambas as
velocidades 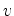 e e 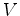 muito menores do que
muito menores do que 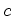 , esta fórmula reduz-se à forma de
Galileu
, esta fórmula reduz-se à forma de
Galileu 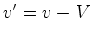 .
.
Note ainda que se 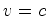 então: então:
|
|

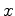 nas mesmas equações
se obtem:
nas mesmas equações
se obtem:
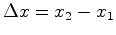
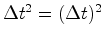 ,
etc...) é um invariante das
transformações de Lorentz, a que se
chama a separação (espaço-temporal) entre os dois
acontecimentos
,
etc...) é um invariante das
transformações de Lorentz, a que se
chama a separação (espaço-temporal) entre os dois
acontecimentos 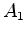 e
e 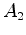 .
.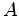 um acontecimento e suponhamos que:
um acontecimento e suponhamos que: 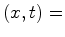 coordenadas de
coordenadas de  .
. 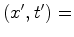 coordenadas de
coordenadas de  , em movimento uniforme com velocidade
, em movimento uniforme com velocidade 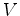 , relativamente a
, relativamente a 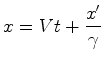
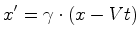
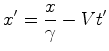
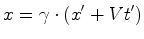
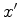 nas
equações (
nas
equações (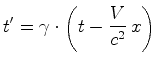
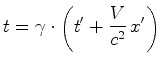
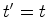 da relatividade de Galileu
(tempo absoluto).
da relatividade de Galileu
(tempo absoluto). 
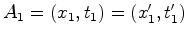 e
e 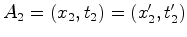 . Usando as fórmulas
anteriores, obtemos:
. Usando as fórmulas
anteriores, obtemos: 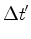
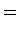
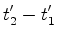
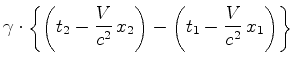
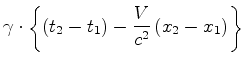
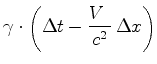
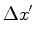
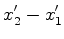
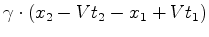
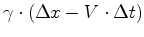
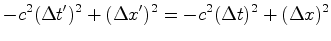
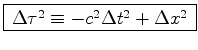
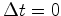 e
e 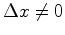 .
. 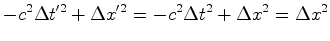
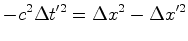
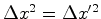 o que só
pode ocorrer quando
o que só
pode ocorrer quando 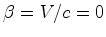 .
.
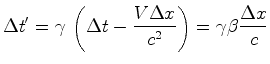
 ,
é menor do que a separação temporal entre
esses mesmos
acontecimentos, medida por observadores ligados a um outro referencial
,
é menor do que a separação temporal entre
esses mesmos
acontecimentos, medida por observadores ligados a um outro referencial 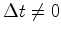 e
e 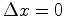 .
. 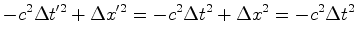
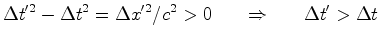
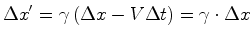
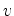 , medida relativamente a um referencial
, medida relativamente a um referencial 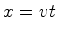
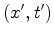 , relativas a um outro referencial
, relativas a um outro referencial 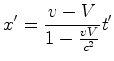
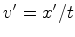 dada por:
dada por:
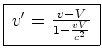
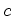 , esta fórmula reduz-se à forma de
Galileu
, esta fórmula reduz-se à forma de
Galileu 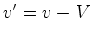 .
. 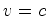 então:
então: