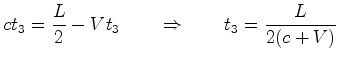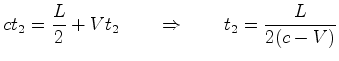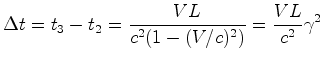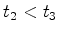|
Dois observadores 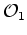 e e 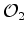 , em repouso relativamente a um
referencial de inércia
, em repouso relativamente a um
referencial de inércia  , possuem cada um o seu relógio. Como é que esses
observadores podem sincronizar os respectivos relógios (isto
é,
no instante em que um marca 0
, por exemplo, o outro marca também
0
) ?
, possuem cada um o seu relógio. Como é que esses
observadores podem sincronizar os respectivos relógios (isto
é,
no instante em que um marca 0
, por exemplo, o outro marca também
0
) ?
Uma
maneira de fazer isso é a seguinte - quando o relógio de 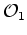 marca
marca 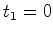 ,
, 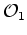 emite um raio luminoso em direcção
a
emite um raio luminoso em direcção
a 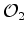 . Este raio percorre uma distância igual a
. Este raio percorre uma distância igual a 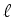 (=
distância entre (=
distância entre 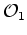 e e 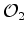 ) com uma velocidade
) com uma velocidade 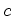 e, por
isso, demora e, por
isso, demora 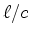 a chegar a a chegar a 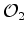 . Se o relógio de
. Se o relógio de 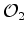 marcar
marcar 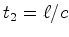 quando
fôr atingido pelo raio, ele marcava quando
fôr atingido pelo raio, ele marcava 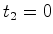 quando o raio
partiu de quando o raio
partiu de 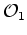 . Portanto os dois relógios
estarão sincronizados.
. Portanto os dois relógios
estarão sincronizados.
O que significa dizer que um
certo acontecimento ocorre num determinado
lugar e num determinado momento, relativamente a um dado referencial de
inércia??
Imaginamos esse referencial
de inércia como um reticulado formado por réguas
graduadas e por um conjunto de relógios, sincronizados entre si,
situados nos vértices do reticulado tridimensional:

As coordenadas
espaço-temporais do acontecimento são um conjunto
ordenado de 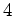 números: um que
especifica o tempo do acontecimento,
registado pelo relógio situado no local onde ocorre, e os
restantes números: um que
especifica o tempo do acontecimento,
registado pelo relógio situado no local onde ocorre, e os
restantes  que
especificam a colocação espacial do acontecimento
relativamente ao
reticulado referido. que
especificam a colocação espacial do acontecimento
relativamente ao
reticulado referido.
Suponhamos
agora que temos dois observadores 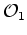 e e 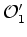 , o
primeiro em repouso relativamente a um referencial de inércia
, o
primeiro em repouso relativamente a um referencial de inércia  , e o segundo em
repouso relativamente a um outro referencial de inércia
, e o segundo em
repouso relativamente a um outro referencial de inércia  , que se desloca com
velocidade uniforme
, que se desloca com
velocidade uniforme 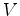 relativamente a relativamente a  . Cada um possui o
seu relógio.
. Cada um possui o
seu relógio.
Será possível
que estes observadores sincronizem os
respectivos relógios ?
|
|
|
A relatividade obriga-nos a rejeitar o
conceito de tempo absoluto!
Num mundo onde o tempo é absoluto, observadores em diferentes
referenciais, usando relógios idênticos, medem sempre
intervalos de
tempo iguais entre dois mesmos acontecimentos. Em particular, se os
dois
acontecimentos são simultâneos para um observador,
serão
também simultâneos para um qualquer outro observador.
No entanto, em relatividade
isto não é assim. Para explicar este facto surpreendente,
analisemos a seguinte experiência conceptual.
Consideremos
um autocarro que se move com velocidade constante 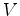 relativamente à paragem.
Seja relativamente à paragem.
Seja  um referencial ligado
à
paragem e um referencial ligado
à
paragem e  um referencial ligado
ao autocarro. um referencial ligado
ao autocarro.
Sejam
 e e 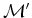 três passageiros dentro do
autocarro, colocados, respectivamente, na parte da frente, na parte de
trás e no meio do autocarro. três passageiros dentro do
autocarro, colocados, respectivamente, na parte da frente, na parte de
trás e no meio do autocarro.
Num
dado instante 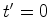 ,
, 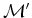 dispara um flash
que emite dois raios luminosos, dispara um flash
que emite dois raios luminosos,  e e  , que seguem em direcções opostas até atingirem os
dois passageiros colocados nos topos do autocarro.
, que seguem em direcções opostas até atingirem os
dois passageiros colocados nos topos do autocarro.
Consideremos os acontecimentos:
 Analisemos
a experiência no referencial Analisemos
a experiência no referencial  :
:
Sejam
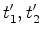 e e 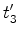 os instantes em que ocorrem
cada um
dos três acontecimentos anteriores (registados pelos
relógios
sincronizados que cada passageiro possui). Como os instantes em que ocorrem
cada um
dos três acontecimentos anteriores (registados pelos
relógios
sincronizados que cada passageiro possui). Como  e e 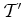 estão à mesma distância de
estão à mesma distância de 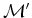 , os raios, viajando à
mesma velocidade, demoram o mesmo tempo a atingir
, os raios, viajando à
mesma velocidade, demoram o mesmo tempo a atingir  e e 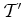 .
Portanto:
.
Portanto:
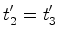
Os
acontecimentos 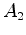 e e 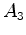 são pois
simultâneos no referencial são pois
simultâneos no referencial  , ligado ao autocarro. , ligado ao autocarro.
 Vejamos
agora como descrever os
mesmos acontecimentos relativamente ao referencial Vejamos
agora como descrever os
mesmos acontecimentos relativamente ao referencial  ligado
à paragem. ligado
à paragem.
O
observador 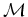 , situado no centro da paragem, testemunha o disparo do flash e a
emissão
dos raios, enquanto que os observadores
, situado no centro da paragem, testemunha o disparo do flash e a
emissão
dos raios, enquanto que os observadores  e e 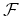 testemunham a
chegada de cada raio aos topos do autocarro. testemunham a
chegada de cada raio aos topos do autocarro.
Sejam 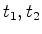 e
e 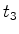 os instantes em que ocorrem cada um dos
três acontecimentos anteriores (registados pelos relógios
sincronizados
que cada testemunha, na paragem, possui). Podemos supôr que
os instantes em que ocorrem cada um dos
três acontecimentos anteriores (registados pelos relógios
sincronizados
que cada testemunha, na paragem, possui). Podemos supôr que 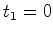 . .
Para as testemunhas na
paragem, o
autocarro move-se com velocidade 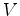 . Analisemos a experiência,
primeiro de acordo com a relatividade de Galileu e depois de
acordo com a relatividade de Einstein.
. Analisemos a experiência,
primeiro de acordo com a relatividade de Galileu e depois de
acordo com a relatividade de Einstein.
-
- Relatividade de Galileu
...
-
Ao
fim do intervalo de tempo 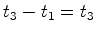 (recorde que fizemos (recorde que fizemos 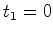 ), o autocarro percorre uma distância
), o autocarro percorre uma distância 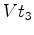 . Seja
. Seja 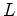 o
comprimento do autocarro (medido em o
comprimento do autocarro (medido em  ). A distância que o
raio 2 percorre, medida em
). A distância que o
raio 2 percorre, medida em  , é igual a
, é igual a 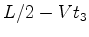 .
.
Por outro lado, essa
mesma distância é igual a 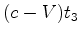 , uma vez que, de acordo com a relatividade de Galileu, a
velocidade do raio
, uma vez que, de acordo com a relatividade de Galileu, a
velocidade do raio 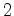 é é 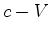 . Portanto:
. Portanto:
-
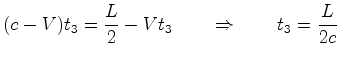 |
(14) |
-
Anàlogamente,
segundo  , a velocidade do raio
, a velocidade do raio 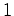 é é 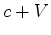 e a distância por ele
percorrida é e a distância por ele
percorrida é  . Portanto:
. Portanto:
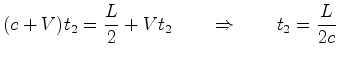 |
(15) |
-
De acordo com a relatividade de Galileu 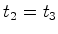 e os dois
acontecimentos são simultâneos em ambos os referenciais. e os dois
acontecimentos são simultâneos em ambos os referenciais.
-
-
-
-
- Relatividade de Einstein ...
Mas a
situação altera-se se adoptarmos o segundo
princípio de
Einstein segundo o qual a velocidade da luz é 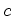 , em ambos os
referenciais. Agora vem que:
, em ambos os
referenciais. Agora vem que:
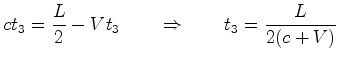 |
(16) |
e,
anàlogamente:
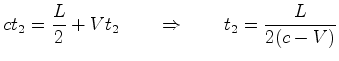 |
(17) |
A
diferença é:
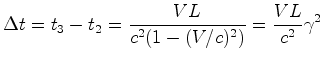 |
(18) |
e:
Conclusão: os acontecimentos 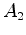 e
e 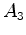 não
são simultâneos, quando descritos no referencial
não
são simultâneos, quando descritos no referencial  , ligado à
paragem !!
, ligado à
paragem !!
Note que não assumimos que as testemunhas na paragem
e os
passageiros no autocarro estão de acordo àcerca do
comprimento
deste. De facto, isso não acontece, como veremos em breve. No
entanto todos concordam que o flash dispara no meio do autocarro.
Concluindo:
Acontecimentos que
ocorrem no mesmo instante mas em locais diferentes, de acordo com um
referencial  (ou o
correspondente conjunto de observadores), ocorrem em instantes
diferentes de acordo com um referencial (ou o
correspondente conjunto de observadores), ocorrem em instantes
diferentes de acordo com um referencial  em movimento relativamente
ao primeiro. em movimento relativamente
ao primeiro. |
Não se questiona o
princípio da causalidade - a causa precede
sempre o efeito - como veremos em breve.
|
|
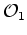 e
e 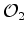 , em repouso relativamente a um
referencial de inércia
, em repouso relativamente a um
referencial de inércia  , possuem cada um o seu relógio. Como é que esses
observadores podem sincronizar os respectivos relógios (isto
é,
no instante em que um marca 0
, por exemplo, o outro marca também
0
) ?
, possuem cada um o seu relógio. Como é que esses
observadores podem sincronizar os respectivos relógios (isto
é,
no instante em que um marca 0
, por exemplo, o outro marca também
0
) ? 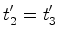
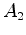 e
e 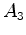 são pois
simultâneos no referencial
são pois
simultâneos no referencial  , ligado ao autocarro.
, ligado ao autocarro. 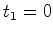 ,
, 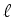 (=
distância entre
(=
distância entre 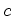 e, por
isso, demora
e, por
isso, demora 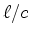 a chegar a
a chegar a 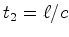 quando
fôr atingido pelo raio, ele marcava
quando
fôr atingido pelo raio, ele marcava 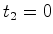 quando o raio
partiu de
quando o raio
partiu de 
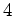 números: um que
especifica o tempo do acontecimento,
registado pelo relógio situado no local onde ocorre, e os
restantes
números: um que
especifica o tempo do acontecimento,
registado pelo relógio situado no local onde ocorre, e os
restantes  que
especificam a colocação espacial do acontecimento
relativamente ao
reticulado referido.
que
especificam a colocação espacial do acontecimento
relativamente ao
reticulado referido. 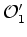 , o
primeiro em repouso relativamente a um referencial de inércia
, o
primeiro em repouso relativamente a um referencial de inércia 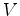 relativamente a
relativamente a  e
e 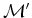 três passageiros dentro do
autocarro, colocados, respectivamente, na parte da frente, na parte de
trás e no meio do autocarro.
três passageiros dentro do
autocarro, colocados, respectivamente, na parte da frente, na parte de
trás e no meio do autocarro. 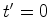 ,
, 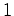 e
e 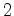 , que seguem em direcções opostas até atingirem os
dois passageiros colocados nos topos do autocarro.
, que seguem em direcções opostas até atingirem os
dois passageiros colocados nos topos do autocarro. 
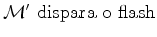
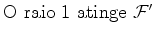
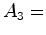
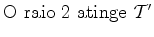
 Analisemos
a experiência no referencial
Analisemos
a experiência no referencial 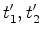 e
e 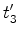 os instantes em que ocorrem
cada um
dos três acontecimentos anteriores (registados pelos
relógios
sincronizados que cada passageiro possui). Como
os instantes em que ocorrem
cada um
dos três acontecimentos anteriores (registados pelos
relógios
sincronizados que cada passageiro possui). Como  e
e 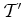 estão à mesma distância de
estão à mesma distância de 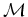 , situado no centro da paragem, testemunha o disparo do flash e a
emissão
dos raios, enquanto que os observadores
, situado no centro da paragem, testemunha o disparo do flash e a
emissão
dos raios, enquanto que os observadores  e
e 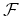 testemunham a
chegada de cada raio aos topos do autocarro.
testemunham a
chegada de cada raio aos topos do autocarro. 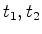 e
e 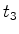 os instantes em que ocorrem cada um dos
três acontecimentos anteriores (registados pelos relógios
sincronizados
que cada testemunha, na paragem, possui). Podemos supôr que
os instantes em que ocorrem cada um dos
três acontecimentos anteriores (registados pelos relógios
sincronizados
que cada testemunha, na paragem, possui). Podemos supôr que 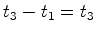 (recorde que fizemos
(recorde que fizemos 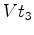 . Seja
. Seja 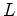 o
comprimento do autocarro (medido em
o
comprimento do autocarro (medido em 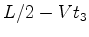 .
. 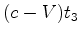 , uma vez que, de acordo com a relatividade de Galileu, a
velocidade do raio
, uma vez que, de acordo com a relatividade de Galileu, a
velocidade do raio 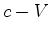 . Portanto:
. Portanto: 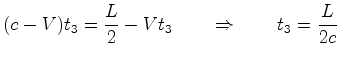
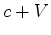 e a distância por ele
percorrida é
e a distância por ele
percorrida é  . Portanto:
. Portanto: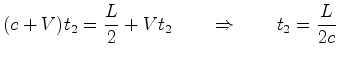
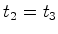 e os dois
acontecimentos são simultâneos em ambos os referenciais.
e os dois
acontecimentos são simultâneos em ambos os referenciais.