|
|
|
|
|
|
|
Nos fins do século XIX, pensava-se que todas as
formas de
movimento ondulatório necessitavam de um meio, através do
qual
se propagariam as ondas. Por exemplo, uma onda sonora, que consiste de
uma série de compressões e rarefações do
ar, que se
sucedem alternadamente, propaga-se através da
transferência de
energia de uma molécula de ar para uma próxima, na
direcção
do movimento da onda através do ar.
Quando Maxwell mostrou, em 1864, que a luz era um
fenómeno
electromagnético ondulatório, pensou-se num meio, a que
se
chamou o "éter", que suportaria a propagação
dessas ondas.
Em 1881, numa experiência célebre, realizada
por A. A. Michelson
e, mais tarde, em 1887, por Edward Morley, tentou medir-se a
velocidade do movimento relativo da terra relativamente ao éter
-
o referido meio imaterial hipotético, através
do qual se
propagariam as ondas electromagnéticas (luz). Baseia-se no
princípio usual da adição de velocidades.
Antes de descrever a experiência de
Michelson-Morley, vejamos uma
analogia sugestiva.
|
|
|
|
|
| Uma
analogia: |
|
Suponhamos que um
barco
navega num lago no qual lançamos uma pedra que provoca uma
ondulação da água do lago.
Relativamente a um
referencial fixo ao lago, as ondas movem-se com uma
velocidade constante, igual a 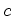 , em todas as
direcções a
partir do ponto de impacto da pedra. , em todas as
direcções a
partir do ponto de impacto da pedra.
Como é que
um ocupante do barco poderá saber se este está ou
não em repouso, relativamente ao lago? E
como
é que ele poderá medir a velocidade 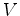 do barco
(relativamente ao lago)? do barco
(relativamente ao lago)?
Para esse ocupante, a velocidade das
ondas à sua volta, depende da direcção da
trajectória do
barco - as ondas que se movem na direcção
do movimento do barco parecem mais lentas, enquanto as que se movem
em direcção contrária parecem mais rápidas.
Portanto, o ocupante do barco pode usar o movimento das
ondas para detectar se o barco se move relativamente ao lago.
Se o ocupante vê
que as ondas em diferentes direcções
viajam todas à velocidade 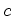 , ele pode concluir que o barco
está parado relativamente ao lago. No entanto, se ele vê
que uma
certa onda viaja com velocidade
, ele pode concluir que o barco
está parado relativamente ao lago. No entanto, se ele vê
que uma
certa onda viaja com velocidade 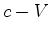 e a onda, na
direcção
oposta, com velocidade
e a onda, na
direcção
oposta, com velocidade 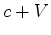 , ele conclui que o barco viaja com
velocidade
, ele conclui que o barco viaja com
velocidade 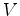 relativamente
ao lago e na direcção da
primeira onda. relativamente
ao lago e na direcção da
primeira onda.
Na experiência de
Michelson-Morley o barco é a terra, a
água
do lago o éter e as ondas são os raios luminosos.
|
|
|
|
|
|
| Descrição
da experiência de Michelson-Morley: |
|
|
|
O objectivo da
experiência é medir a velocidade da
"corrente de
éter" através do aparelho, chamado interferómetro
de
Michelson-Morley (ligado à terra) que se ilustra no appplett
seguinte:
A analogia com o exemplo dos
nadadores, que vimos na secção
anterior, é flagrante - em vez dos nadadores usam-se dois feixes
luminosos, e em vez das margens do rio, um conjunto de espelhos e um
detector. A água é o hipotético éter.
Uma lâmpada 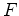 emite um feixe de luz monocromático que
atinge
um espelho semi-prateado emite um feixe de luz monocromático que
atinge
um espelho semi-prateado 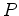 , inclinado, que reflecte cerca de
metade da luz incidente e transmite a restante. O raio transmitido
atinge um espelho reflector
, inclinado, que reflecte cerca de
metade da luz incidente e transmite a restante. O raio transmitido
atinge um espelho reflector 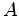 e é reflectido de volta para e é reflectido de volta para 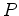 (o nadador
(o nadador 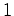 ), onde é novamente parcialmente reflectido e
finalmente atinge um detector
), onde é novamente parcialmente reflectido e
finalmente atinge um detector 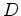 (o raio transmitido não tem
interesse na experiência). (o raio transmitido não tem
interesse na experiência).
A parte reflectida do raio 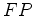 atinge um segundo espelho atinge um segundo espelho 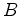 onde
é reflectido de volta para onde
é reflectido de volta para 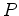 (nadador (nadador 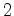 ). A parte transmitida
deste raio atinge o detector
). A parte transmitida
deste raio atinge o detector 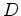 juntamente com o raio que
atravessou o outro trajecto. Os braços juntamente com o raio que
atravessou o outro trajecto. Os braços 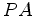 e e 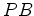 têm o mesmo
comprimento têm o mesmo
comprimento 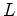 , e o aparelho é montado sobre uma plataforma
giratória.
, e o aparelho é montado sobre uma plataforma
giratória.
Se a terra se move
relativamente ao éter, ou, de forma
equivalente, se existir uma "corrente de éter" que atravessa o
aparelho, a velocidade da luz é diferente ao longo de cada um
dos
braços do aparelho. Como o primeiro segmento 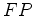 e o último e o último 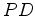 são comuns a ambos os
trajectos, a diferença é
determinada pelos tempos são comuns a ambos os
trajectos, a diferença é
determinada pelos tempos 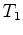 , do trajecto
, do trajecto 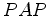 (nadador (nadador 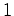 ),
e
),
e 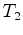 do trajecto do trajecto 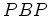 (nadador (nadador 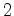 ):
):
Note que 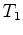 e e 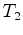 devem ser os mesmos em ambos
os referenciais, o
ligado à terra e o ligado ao éter - a coordenada temporal
não
se altera sob uma transformação de Galileu. devem ser os mesmos em ambos
os referenciais, o
ligado à terra e o ligado ao éter - a coordenada temporal
não
se altera sob uma transformação de Galileu.
Se:
-
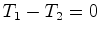 , nenhuma
interferência é observada no detector. , nenhuma
interferência é observada no detector.
-
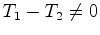 , observa-se
interferência no
detector. , observa-se
interferência no
detector.
Esta inteferência
pode ser de dois tipos:
- construtiva:

- destrutiva:

|
|
|
Se:
- 1.
- o
braço
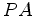 está alinhado com a
direcção da corrente de
éter, o sinal está alinhado com a
direcção da corrente de
éter, o sinal 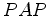 é mais lento que o sinal é mais lento que o sinal 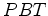 :
: 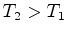 , e a diferença máxima é:
, e a diferença máxima é:
-
No detector observa-se um padrão de
interferência com
faixas pretas e brancas, com largura:
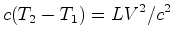 |
(11) |
FIGURA
- 2.
- o interferómetro
é rodado, a diferença nos tempos de
percurso dos sinais
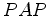 e e 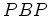 decresce até zero (quando ambos
os braços formam um ângulo de decresce até zero (quando ambos
os braços formam um ângulo de 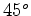 relativamente à
corrente de éter) e depois começa a aumentar. O sinal relativamente à
corrente de éter) e depois começa a aumentar. O sinal 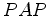 fica mais rápido do que o sinal
fica mais rápido do que o sinal 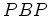 .
.
No detector observa-se
que as faixas pretas e brancas começam a
deslocar-se e passam a marca. A largura das faixas diminui (até
zero: 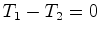 ), e começa depois a aumentar.
), e começa depois a aumentar.
-
FIGURA
- 3.
- o
braço
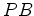 fica agora alinhado com a direcção
da corrente de
éter, e sinal fica agora alinhado com a direcção
da corrente de
éter, e sinal 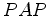 é mais rápido do que o sinal é mais rápido do que o sinal 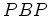 :
: 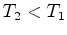 , e a diferença máxima é:
, e a diferença máxima é:
-
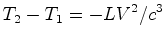 |
(12) |
-
No detector observa-se
que a largura das faixas atinge novamente
um máximo, dado por 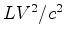 . Algumas faixas passaram além
da marca.
. Algumas faixas passaram além
da marca.
-
FIGURA
A variação das diferenças (11) e (12),
correspondentes às posições 1. e 2.,
é:
Portanto, a largura
máxima do padrão de interferência
observado no detector, é 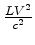 . Podemos medir este
valor, contando o número
. Podemos medir este
valor, contando o número 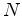 de faixas que passam a marca, à
medida que a largura do padrão varia desde o seu valor
máximo
até zero e aumenta depois até novamente o seu
máximo, e
multiplicando esse número de faixas que passam a marca, à
medida que a largura do padrão varia desde o seu valor
máximo
até zero e aumenta depois até novamente o seu
máximo, e
multiplicando esse número 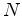 pela largura pela largura 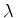 de uma única faixa (i.e., pelo comprimento de
onda dos sinais luminosos):
de uma única faixa (i.e., pelo comprimento de
onda dos sinais luminosos):
Como conhecemos 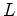 e e 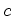 , podemos determinar
, podemos determinar 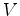 , se conseguirmos
observar um deslocamento de faixas no detector.
, se conseguirmos
observar um deslocamento de faixas no detector.
Mas nenhum
deslocamento desse tipo foi observado !!!
Portanto, experimentalmente, não se observou qualquer
diferença nos tempos de percurso dos sinais 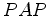 e e 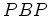 :
:
|
|
| Possíveis
explicações: |
|
|
|
- 1.
- A terra está em repouso relativamente ao
éter -
uma hipótese altamente improvável!!
- 2.
- Contracção
de Lorentz-Fitzgerald - os
objectos sofrem uma contracção física na
direcção do seu
movimento através do éter.
Vejamos como isto poderia explicar o resultado
experimental de que
as duas distâncias seguintes:
- a
distância percorrida pelo sinal 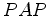 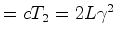 .
.
- a
distância percorrida pelo sinal 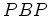 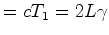 .
.
são iguais: 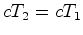 ? ?
-
Suponhamos que o 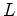 que surge em cada uma das fórmulas
é
diferente: que surge em cada uma das fórmulas
é
diferente:
Isto implicaria que:
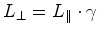 |
(13) |
- isto é, o
comprimento
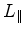 do
braço do interferómetro, paralelo
à direcção do movimento, é mais curto do
que o comprimento do
braço do interferómetro, paralelo
à direcção do movimento, é mais curto do
que o comprimento 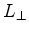 do braço
perpendicular à direcção do movimento
(recorde que do braço
perpendicular à direcção do movimento
(recorde que 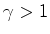 ) !! Mas esta é justamente a hipótese de
Lorentz-Fitzgerald !!
) !! Mas esta é justamente a hipótese de
Lorentz-Fitzgerald !!
-
- 3.
- Postulado de Einstein
A velocidade da luz é a mesma em todos os
referenciais de inércia.
Neste caso, no
referencial ligado à terra, 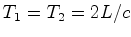 .
.
|
|
|
|
|
|
Página seguinte:
Implicações da nova teoria
Página
anterior: Transformações de Galileu
Índice
|
|

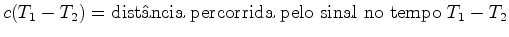
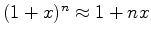 , com
, com 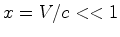 .
Inicialmente suposemos que o braço
.
Inicialmente suposemos que o braço 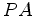 estava alinhado com a
direcção do movimento da terra através do
éter, ou de forma
equivalente, com a direcção da corrente de éter.
Suponhamos
agora que rodamos o interferómetro (ou que admitimos que a
corrente de éter muda de direcção).
estava alinhado com a
direcção do movimento da terra através do
éter, ou de forma
equivalente, com a direcção da corrente de éter.
Suponhamos
agora que rodamos o interferómetro (ou que admitimos que a
corrente de éter muda de direcção).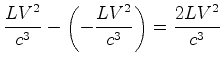
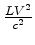 . Podemos medir este
valor, contando o número
. Podemos medir este
valor, contando o número 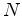 de faixas que passam a marca, à
medida que a largura do padrão varia desde o seu valor
máximo
até zero e aumenta depois até novamente o seu
máximo, e
multiplicando esse número
de faixas que passam a marca, à
medida que a largura do padrão varia desde o seu valor
máximo
até zero e aumenta depois até novamente o seu
máximo, e
multiplicando esse número 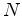 pela largura
pela largura 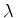 de uma única faixa (i.e., pelo comprimento de
onda dos sinais luminosos):
de uma única faixa (i.e., pelo comprimento de
onda dos sinais luminosos): 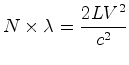
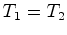
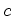 , em todas as
direcções a
partir do ponto de impacto da pedra.
, em todas as
direcções a
partir do ponto de impacto da pedra.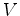 do barco
(relativamente ao lago)?
do barco
(relativamente ao lago)?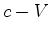 e a onda, na
direcção
oposta, com velocidade
e a onda, na
direcção
oposta, com velocidade 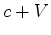 , ele conclui que o barco viaja com
velocidade
, ele conclui que o barco viaja com
velocidade 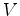 relativamente
ao lago e na direcção da
primeira onda.
relativamente
ao lago e na direcção da
primeira onda. 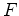 emite um feixe de luz monocromático que
atinge
um espelho semi-prateado
emite um feixe de luz monocromático que
atinge
um espelho semi-prateado 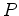 , inclinado, que reflecte cerca de
metade da luz incidente e transmite a restante. O raio transmitido
atinge um espelho reflector
, inclinado, que reflecte cerca de
metade da luz incidente e transmite a restante. O raio transmitido
atinge um espelho reflector 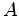 e é reflectido de volta para
e é reflectido de volta para 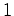 ), onde é novamente parcialmente reflectido e
finalmente atinge um detector
), onde é novamente parcialmente reflectido e
finalmente atinge um detector 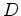 (o raio transmitido não tem
interesse na experiência).
(o raio transmitido não tem
interesse na experiência). 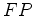 atinge um segundo espelho
atinge um segundo espelho 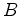 onde
é reflectido de volta para
onde
é reflectido de volta para 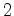 ). A parte transmitida
deste raio atinge o detector
). A parte transmitida
deste raio atinge o detector 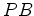 têm o mesmo
comprimento
têm o mesmo
comprimento 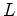 , e o aparelho é montado sobre uma plataforma
giratória.
, e o aparelho é montado sobre uma plataforma
giratória. 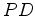 são comuns a ambos os
trajectos, a diferença é
determinada pelos tempos
são comuns a ambos os
trajectos, a diferença é
determinada pelos tempos 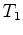 , do trajecto
, do trajecto 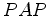 (nadador
(nadador 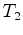 do trajecto
do trajecto 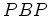 (nadador
(nadador 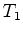
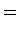
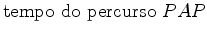
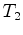
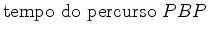
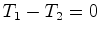 , nenhuma
interferência é observada no detector.
, nenhuma
interferência é observada no detector. 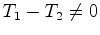 , observa-se
interferência no
detector.
, observa-se
interferência no
detector. 

 , ligado ao aparelho) e
conduzem a (ver as fórmulas
(
, ligado ao aparelho) e
conduzem a (ver as fórmulas
(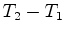
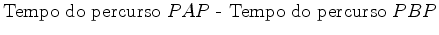
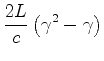
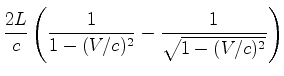
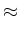
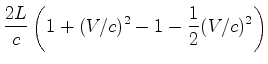
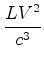
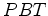 :
: 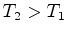 , e a diferença máxima é:
, e a diferença máxima é: 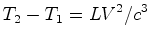
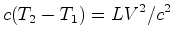
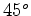 relativamente à
corrente de éter) e depois começa a aumentar. O sinal
relativamente à
corrente de éter) e depois começa a aumentar. O sinal 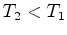 , e a diferença máxima é:
, e a diferença máxima é: 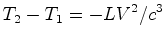
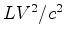 . Algumas faixas passaram além
da marca.
. Algumas faixas passaram além
da marca. 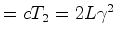 .
. 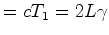 .
. 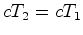 ?
? 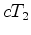
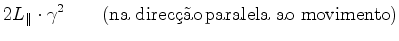
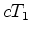
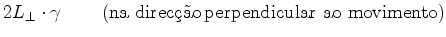
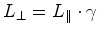
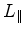 do
braço do interferómetro, paralelo
à direcção do movimento, é mais curto do
que o comprimento
do
braço do interferómetro, paralelo
à direcção do movimento, é mais curto do
que o comprimento 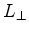 do braço
perpendicular à direcção do movimento
(recorde que
do braço
perpendicular à direcção do movimento
(recorde que 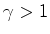 ) !! Mas esta é justamente a hipótese de
Lorentz-Fitzgerald !!
) !! Mas esta é justamente a hipótese de
Lorentz-Fitzgerald !! 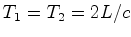 .
.