Relatividade Restrita - Uma introdução
Contracção do comprimento |
||||||||||||
 |
||||||||||||
|
Considere mais uma vez um
autocarro que se move com velocidade
constante
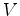 relativamente à paragem.
Seja relativamente à paragem.
Seja  um referencial
ligado à paragem e um referencial
ligado à paragem e  um referencial ligado ao autocarro. um referencial ligado ao autocarro.
Um
observador 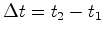 que
separa os dois instantes
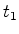 e e 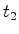 em que a parte da frente e a
parte de trás do autocarro passam no centro da paragem -
acontecimentos em que a parte da frente e a
parte de trás do autocarro passam no centro da paragem -
acontecimentos 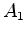 e e 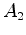 , respectivamente:
, respectivamente:
Como o autocarro se move
com velocidade
Para
medir o comprimento 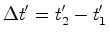 Relativamente a estes passageiros, a paragem move-se com
velocidade
Mas
o intervalo
e daí que: 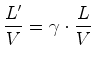 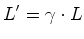 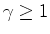 , tem-se que:
, tem-se que:
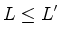 |
||||||||||||
| Concluindo: | ||||||||||||
|
|
||||||||||||
| Página seguinte: Efeito Doppler Página anterior: Dilatação do tempo Índice |
 , fixo no centro da paragem,
pode medir o comprimento
, fixo no centro da paragem,
pode medir o comprimento 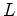 do autocarro, de acordo com o seu
referencial
do autocarro, de acordo com o seu
referencial 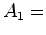
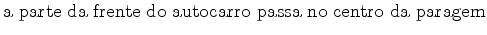
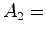
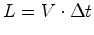
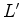 do autocarro, de acordo com o
referencial
do autocarro, de acordo com o
referencial 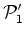 e
e 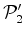 ,
dentro do autocarro, um na parte da frente e outro na parte
traseira, registam, com os respectivos relógios, os dois
instantes
,
dentro do autocarro, um na parte da frente e outro na parte
traseira, registam, com os respectivos relógios, os dois
instantes 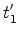 e
e 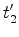 , em que a parte da frente e a parte de trás
passam no centro da paragem - os mesmos acontecimentos
, em que a parte da frente e a parte de trás
passam no centro da paragem - os mesmos acontecimentos 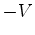 . Logo:
. Logo: 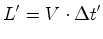
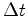 é o tempo
próprio entre os dois acontecimentos
é o tempo
próprio entre os dois acontecimentos 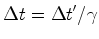
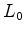 . No exemplo anterior,
. No exemplo anterior, 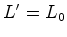 é o
comprimento próprio do autocarro. O comprimento próprio
é
sempre maior do que o comprimento medido num qualquer outro referencial:
é o
comprimento próprio do autocarro. O comprimento próprio
é
sempre maior do que o comprimento medido num qualquer outro referencial: