|
Os efeitos Doppler para o
som e para a luz diferem num ponto crucial
- as ondas sonoras propagam-se num meio (ar), enquanto que as
luminosas não (não existe o éter).
Portanto, no caso sonoro,
podemos distinguir o movimento do emissor do do receptor (observador) -
"emissor em movimento" ou "receptor em movimento" significa sempre
movimento relativo ao meio.
No caso luminoso não
existe uma tal distinção. A única coisa
com significado é o movimento relativo do emissor e do receptor.
Suponhamos
então que um emissor 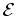 emite luz. Para
visualizarmos a onda luminosa, representá-mo-la por uma
sucessão regular de pulsos pontuais, emanando de emite luz. Para
visualizarmos a onda luminosa, representá-mo-la por uma
sucessão regular de pulsos pontuais, emanando de 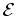 (ver o
applett). (ver o
applett).
Suponhamos
que a frequência da onda, medida no referencial de repouso,  , do emissor, é: , do emissor, é:
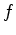 = número de pulsos pontuais
que
passam numa certa secção fixa de = número de pulsos pontuais
que
passam numa certa secção fixa de  , por unidade de tempo
(segundo, por exemplo).
, por unidade de tempo
(segundo, por exemplo).
Dois pulsos consecutivos distam 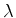 um do
outro, isto é, um do
outro, isto é, 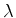 é o respectivo comprimento de
onda (medido
em é o respectivo comprimento de
onda (medido
em  ).
).
A
luz é detectada por um observador (receptor)  , que se
afasta do emissor
, que se
afasta do emissor 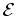 com uma velocidade relativa com uma velocidade relativa 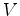 .
.
Pretendemos calcular a frequência 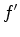 detectada pelo receptor,
isto é, o número de pulsos que o atingem por segundo,
medida no
seu referencial de repouso detectada pelo receptor,
isto é, o número de pulsos que o atingem por segundo,
medida no
seu referencial de repouso  .
.
- O applett seguinte mostra a
experiência descrita no
referencial de repouso
 do emissor. do emissor.
No
instante 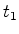 o pulso o pulso 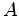 atinge o receptor (acontecimento atinge o receptor (acontecimento 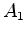 ) e no instante
) e no instante 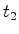 o
pulso seguinte o
pulso seguinte 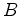 atinge o receptor (acontecimento atinge o receptor (acontecimento 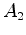 ), que
entretanto se afastou do emissor uma distância igual a
), que
entretanto se afastou do emissor uma distância igual a 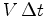 , onde
, onde 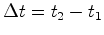 é o intervalo entre os
acontecimentos
é o intervalo entre os
acontecimentos 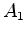 e e 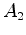 (medido em (medido em  ).
).
-
A distância entre
os pulsos 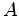 e e 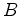 é igual ao comprimento da
onda é igual ao comprimento da
onda 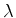 que, por sua vez,
é igual a: que, por sua vez,
é igual a:
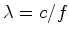 |
(29) |
(medido
em  ).
).
No
intervalo de tempo 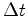 cada pulso moveu-se cada pulso moveu-se 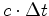 . Portanto (ver o applett):
. Portanto (ver o applett):
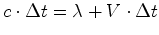 |
(30) |
isto é:
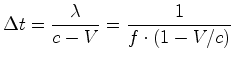 |
(31) |
Se o receptor se aproxima do emissor, uma
análise semelhante
mostra que:
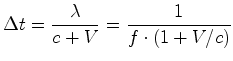 |
(32) |
É
claro que o que nos interessa é o intervalo 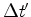 entre
os acontecimentos entre
os acontecimentos 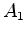 e e 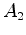 , medido agora no referencial de repouso
, medido agora no referencial de repouso  do
receptor. Como os acontecimentos do
receptor. Como os acontecimentos 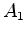 e e 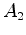 ocorrem no mesmo local de ocorrem no mesmo local de  (ver o applett), sabemos que (ver o applett), sabemos que 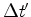 é o intervalo de
tempo próprio e, por isso: é o intervalo de
tempo próprio e, por isso:
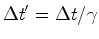 |
(33) |
A frequência 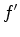 é o recíproco de é o recíproco de 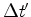 , e portanto,
usando as fórmulas anteriores, obtemos:
, e portanto,
usando as fórmulas anteriores, obtemos:
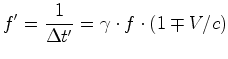 |
(34) |
onde o sinal - se refere ao
caso em que o receptor e o emissor se afastam e o sinal + ao caso em
que se aproximam.
Uma pequena manipulação
algébrica permite finalmente escrever
as fórmulas seguintes do efeito de Doppler:
 |
(35) |
e:
 |
(36) |
Note que:
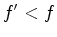 , quando o receptor e emissor se
afastam - desvio para o
vermelho (redshift). , quando o receptor e emissor se
afastam - desvio para o
vermelho (redshift). 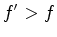 , quando o receptor e emissor se
aproximam - desvio para o
azul (blueshift). , quando o receptor e emissor se
aproximam - desvio para o
azul (blueshift).
|
|

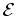 emite luz. Para
visualizarmos a onda luminosa, representá-mo-la por uma
sucessão regular de pulsos pontuais, emanando de
emite luz. Para
visualizarmos a onda luminosa, representá-mo-la por uma
sucessão regular de pulsos pontuais, emanando de  , do emissor, é:
, do emissor, é: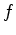 = número de pulsos pontuais
que
passam numa certa secção fixa de
= número de pulsos pontuais
que
passam numa certa secção fixa de 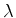 um do
outro, isto é,
um do
outro, isto é,  , que se
afasta do emissor
, que se
afasta do emissor 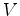 .
.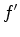 detectada pelo receptor,
isto é, o número de pulsos que o atingem por segundo,
medida no
seu referencial de repouso
detectada pelo receptor,
isto é, o número de pulsos que o atingem por segundo,
medida no
seu referencial de repouso  .
.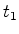 o pulso
o pulso 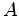 atinge o receptor (acontecimento
atinge o receptor (acontecimento 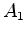 ) e no instante
) e no instante 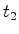 o
pulso seguinte
o
pulso seguinte 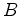 atinge o receptor (acontecimento
atinge o receptor (acontecimento 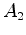 ), que
entretanto se afastou do emissor uma distância igual a
), que
entretanto se afastou do emissor uma distância igual a 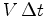 , onde
, onde 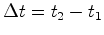 é o intervalo entre os
acontecimentos
é o intervalo entre os
acontecimentos 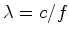
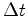 cada pulso moveu-se
cada pulso moveu-se 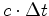 . Portanto (ver o applett):
. Portanto (ver o applett): 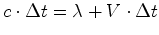
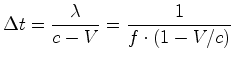
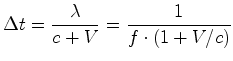
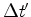 entre
os acontecimentos
entre
os acontecimentos 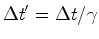
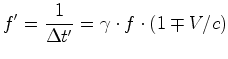


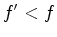 , quando o receptor e emissor se
afastam -
, quando o receptor e emissor se
afastam - 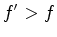 , quando o receptor e emissor se
aproximam -
, quando o receptor e emissor se
aproximam -