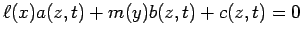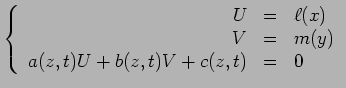| O que é a Nomografia? |
||||||
| Next: A
equação cúbica completa Previous:
Nomogramas de
alinhamento para Índice |
||||||
|
Suponhámos que numa equação do tipo (12), substituímos as funções de uma variável por funções de duas variáveis, obtendo assim a equaçãode seis variáveis: Para representar
nomogràficamente esta equação considerámos
as três famílias a É claro que cada
uma delas pode ser definida pelas coordenadas
cartesianas 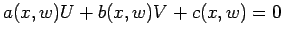 que define uma rede de curvas no plano 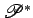 , a que
chamámos a
rede , a que
chamámos a
rede 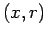 . De
facto, eliminando nestas duas equações primeiro . De
facto, eliminando nestas duas equações primeiro 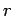 e depois e depois 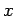 , obtemos duas famílias de curvas
definidas
implicitamente por: , obtemos duas famílias de curvas
definidas
implicitamente por: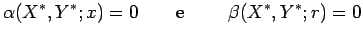 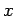 e a segunda por e a segunda por 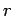 . Para um par dado destes parâmetros . Para um par dado destes parâmetros 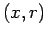 , o ponto
bicotado , o ponto
bicotado 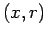 não é mais do que a intersecção das curvas
cotadas
não é mais do que a intersecção das curvas
cotadas 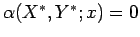 e e
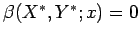 . .
Tendo construído
desta forma as três redes
Uma ou mais destas redes
podem ser degeneradas, no sentido em que
o suporte dos pontos (35),
pode reduzir-se a uma
mesma curva no plano  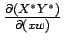 tem rank
tem rank 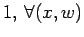 . .
Entre os nomogramas com
pontos alinhados com duas cotas, os mais
frequentes na prática são os constituídos por uma
única
rede bicotada e por duas outras escalas com uma só cota. As
equações representáveis por nomogramas deste tipo
são da
forma:
Para construir o respectivo nomograma pômos:

Next: A equação cúbica completa Previous: Nomogramas de alinhamento para Índice Joao Nuno Tavares 2005-03-28 |
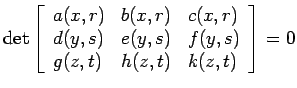
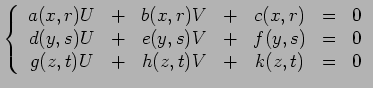
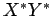 , definidas em
, definidas em
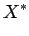
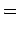
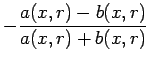
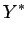
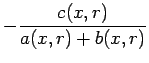
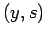 e
e 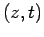 , vemos
que a representação nomográfica da
equação
(
, vemos
que a representação nomográfica da
equação
(
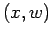 , quando
, quando