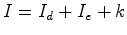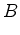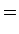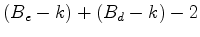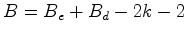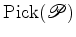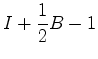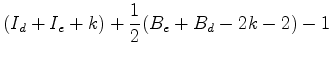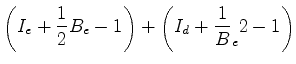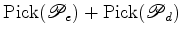O Teorema de Pick e o cálculo da área de polígonos
Seja 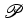 um polígono cujos
vértices são pontos do
reticulado um polígono cujos
vértices são pontos do
reticulado 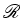 .
.
Aos pontos que estão sobre as arestas do polígono chamamos pontos fronteira e aos que estão no interior do polígono chamamos pontos interiores. O
polígono
|
||||||||||||||||||
O teorema seguinte foi
descoberto em 1899 por Georg
Alexander Pick e permite
calcular a área de um polígono simples contando o
número 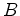 dos seus pontos de fronteira e o número
dos seus pontos de fronteira e o número 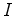 dos
seus pontos
interiores. dos
seus pontos
interiores.
|
||||||||||||||||||
|
O Teorema de Pick é fascinante porque nos permite calcular a área de um polígono simples a partir da contagem de pontos do reticulado. É de facto surpreendente que seja possível substituir o processo habitual de cálculo de uma área, que envolve medições de grandezas contínuas, por uma contagem de grandezas discretas (uma espécie de "quantização" da área!) |
||||||||||||||||||
| Demonstração do teorema de
Pick |
||||||||||||||||||
|
Para demonstrarmos o
teorema
de Pick, vamos mostrar, em primeiro
lugar, que o segundo membro da fórmula de Pick - o que dá
aquilo
a que podemos chamar o número de Pick do polígono
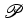 : :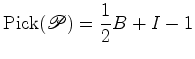 é aditivo
no sentido seguinte: justapondo dois
polígonos
ao longo de pelo menos uma aresta, então o número de Pick
do
polígono resultante é igual à soma dos
números de Pick dos
dois polígonos referidos.
Este facto não deve surpreender. De facto, como sabemos, o mesmo acontece para área - justapondo dois polígonos ao longo de pelo menos uma aresta, a área do polígono obtido é a soma das áreas dos polígonos iniciais. Assim, se o Teorema de Pick for válido, por outras palavras, se: 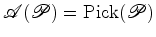 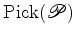 terá de
obedecer a essa mesma
propriedade de aditividade.
terá de
obedecer a essa mesma
propriedade de aditividade. |
||||||||||||||||||
A prova de que o número de Pick é aditivo está sugerida na animação seguinte: |
||||||||||||||||||
Consideremos
então dois polígonos arbitrários 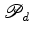 e e 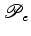 ,
sendo ,
sendo 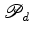 o
polígono da
direita e o
polígono da
direita e 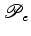 o
da esquerda. o
da esquerda. Suponhamos
que o número de pontos do interior e da fronteira do
polígono
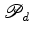 são são 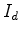 e
e 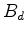 , respectivamente, e os
do polígono
, respectivamente, e os
do polígono 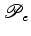 são são 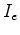 e e 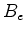 . Unindo os
polígonos
. Unindo os
polígonos 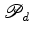 e e 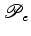 obtemos um
polígono obtemos um
polígono 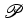 com com 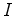 pontos interiores e pontos interiores e 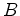 pontos de
fronteira, como se ilustra na figura anterior. O nosso objectivo
é pois mostrar que: pontos de
fronteira, como se ilustra na figura anterior. O nosso objectivo
é pois mostrar que:
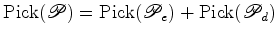 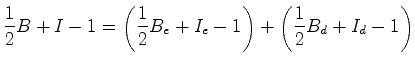
Repare
que, depois de justapôr os dois polígonos, os
pontos do
reticulado situados sobre as arestas comuns dos dois polígonos Seja
Por
outro lado, se quisermos
calcular Resumindo tudo isto, temos então que: Substituindo
então (1) e (2) na
fórmula de
Está assim provada a aditividade do número de Pick. |
||||||||||||||||||
Exercício: comprove a
aditividade do número de Pick para os polígonos da figura
seguinte: |
||||||||||||||||||
Mas como é que a propriedade da aditividade do número de Pick nos pode ajudar a provar o teorema de Pick? |
||||||||||||||||||
Vejamos! Acabamos de
mostrar
que justapondo dois polígonos ao
longo de pelo menos uma aresta, os respectivos números de Pick
adicionam-se (bem como as respectivas áreas, é claro).
Isto
sugere a seguinte estratégia de demonstração:
decompômos o
polígono dado,
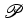 , numa justaposição de polígonos
"elementares" para os quais o teorema de Pick seja fácil de
verificar directamente.
, numa justaposição de polígonos
"elementares" para os quais o teorema de Pick seja fácil de
verificar directamente. Ora,
qualquer polígono
simples 
Basta pois provar o teorema de Pick para um triângulo arbitrário com vértices no reticulado.
Mas um tal triângulo pode ser completado num triângulo rectângulo justapondo-lhe ou rectângulos ou novos triângulos rectângulos. E, por último, um rectângulo é justaposição de dois triângulos rectângulos.
Tudo
isto permite concluir
que basta provar o teorema de Pick para rectângulos! Mas estes
são justaposição de quadrados de lado 1. E para
estes últimos, o teorema de Pick é trivial. De facto.
para um quadrados de lado 1, a área é 1, enquanto que
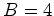 ,
, 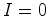 e portanto o número de
Pick é e portanto o número de
Pick é 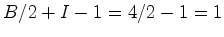 . . |
||||||||||||||||||


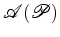
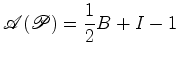
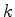 o número de pontos de
contacto de
o número de pontos de
contacto de