Demonstração do Teorema de Polya
|
A demonstração do
teorema
de Polya depende de uma versão
generalizada do Lema de Burnside: |
|||||
|
|||||
Nota:
O lema usual (8)
obtem-se tomando
os
pesos todos iguais a 1 -
 .
. |
|||||
|
Todas as colorações
que
estão na mesma órbita de 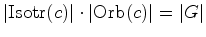 Vemos pois que cada órbita
dá a mesma
contribuição ![$\displaystyle \vert G\vert\cdot \sum_{[c]\in{\mathscr{C}}/G} W([c])=
\sum_{g\in G}\sum_{c\in {\hbox{\small Fix($g$)}}}\, W(c)$](img259.gif)
|
|||||
|
Demonstração
do Teorema
de Polya
Por definição do
inventário de padrões e pelo lema de Burnside, temos que: ![$\displaystyle \hbox{\bf IP}= \sum_{[c]\in {\mathscr{C}}/G}\,
W([c])=\frac{1}{\vert G\vert} \sum_{g\in G}\,\sum_{c\in {\hbox{\small
Fix($g$)}}}\, W(c)$](img260.gif) Recordando a definição (11) do índice de ciclos , resta pois mostrar que: onde 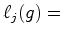 é
o número
de ciclos de comprimento é
o número
de ciclos de comprimento 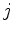 na
decomposição de
na
decomposição de 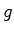 em ciclos
disjuntos.
em ciclos
disjuntos.Fixemos um Suponhamos que 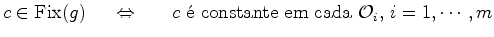 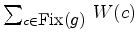 não
é mais do
que a soma: não
é mais do
que a soma:
Recordando que o peso
Suponhamos agora que a
decomposição de
Entre os números  Portanto o produto (29) pode ser escrito na forma: 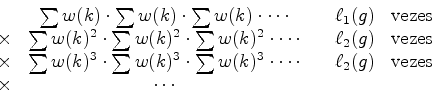 
|
|||||
| Regresso ao texto principal |
|||||
| Página
seguinte Página anterior Índice |

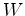
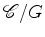 -
- 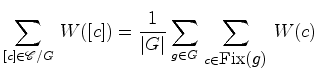
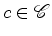 entra na
soma
entra na
soma
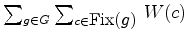 ? Tantas vezes quantas o cardinal
? Tantas vezes quantas o cardinal
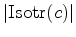 do subgrupo de isotropia de
do subgrupo de isotropia de 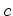 .
. 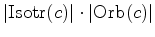 que,
pela fórmula (
que,
pela fórmula (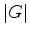 , para a
soma
, para a
soma
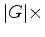 a
soma dos pesos das órbita
a
soma dos pesos das órbita
![$ [c]\in {\mathscr{C}}/G$](img227.gif) ,
isto é:
,
isto é: 

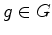 , visto como uma permutação dos objectos
(vértices) de
, visto como uma permutação dos objectos
(vértices) de 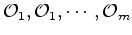 .
Como
já vimos:
.
Como
já vimos:
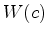 de uma coloração
de uma coloração
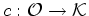 é,
por definição, igual ao produto dos pesos das cores
usadas em
é,
por definição, igual ao produto dos pesos das cores
usadas em 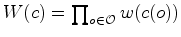 ,
vemos que a soma (
,
vemos que a soma (
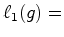 ciclos de comprimento
ciclos de comprimento 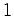 ,
,  ciclos
de comprimento
ciclos
de comprimento  ,
, 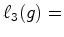 ciclos de comprimento
ciclos de comprimento 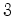 , etc.
, etc. 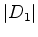 ,
, 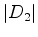 ,
, 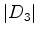 , ...
, ...