|
Consideremos dois planos 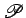 e e 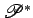 . Uma dualidade ou
correlação entre eles é uma correspondência
do tipo: . Uma dualidade ou
correlação entre eles é uma correspondência
do tipo:
que verifica as propriedades
indicadas no quadro seguinte.
Plano 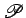 |
|
Plano dual 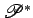 |
Ponto 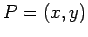 |
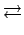 |
Recta 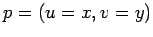 |
Recta 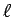 |
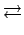 |
Feixe de rectas 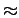 ponto suporte ponto suporte 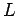 |
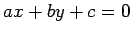 |
|
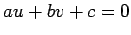 |
| Recta que une dois pontos |
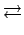 |
Ponto intersecção de duas
rectas |
| 3 rectas intersectam-se num ponto |
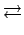 |
3 pontos estão alinhados |
| |
|
sobre uma mesma recta |
| Ponto intersecção de duas
rectas |
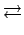 |
Recta que une dois pontos |
| |
|
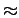 recta comum a dois
feixes recta comum a dois
feixes |
| Curva pontual |
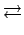 |
Família a um parâmetro de
rectas |
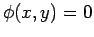 |
|
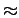 envolvente envolvente 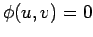 |
Recta tangente à curva num ponto 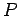 |
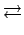 |
Ponto característico da recta
dual a 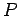 |
| Curvas intersectam-se num ponto |
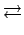 |
Recta tangente comum às curvas
duais |
A realização concreta desta dualidade far-se-á da
seguinte
forma - no plano 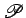 escolhemos um referencial cartesiano escolhemos um referencial cartesiano
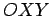 , e no plano , e no plano 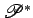 escolhemos duas rectas paralelas
orientadas e uma terceira que intersecte ambas nos pontos escolhemos duas rectas paralelas
orientadas e uma terceira que intersecte ambas nos pontos 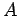 e e
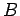 . Ao ponto . Ao ponto 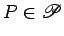 , de coordenadas , de coordenadas 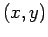 , associámos a
recta , associámos a
recta 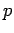 , de , de 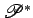 , que une os pontos , que une os pontos 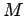 e e 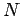 , onde , onde 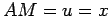 e e
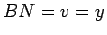 (ambos
marcados de acordo com a orientação definida em
cada recta). (ambos
marcados de acordo com a orientação definida em
cada recta). 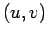 dizem-se as coordenadas
paralelas da recta dizem-se as coordenadas
paralelas da recta
 . .
No applet seguinte, pode
variar com o rato a posiçãodo ponto
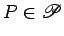 e apreciar a
correspondente variação da recta dual e apreciar a
correspondente variação da recta dual
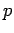 em em 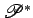 . .
Este ponto 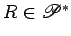 diz-se o dual da recta diz-se o dual da recta 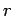 de de 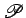 . Como . Como
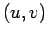 satisfazem
a equação: satisfazem
a equação:
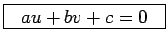 |
(17) |
esta diz-se a equação tangencial do ponto 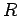 . Simbòlicamente: . Simbòlicamente:
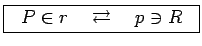 |
(18) |
No
applet seguinte, pode variar com o rato a posiçãoda recta
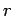 (azul) mexendo nas
intersecções com os eixos coordenados (os pontos vermelho
e verde). Pode depois fazer variar a posição do ponto (azul) mexendo nas
intersecções com os eixos coordenados (os pontos vermelho
e verde). Pode depois fazer variar a posição do ponto 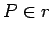 para constatar o
significado da proposição anterior. para constatar o
significado da proposição anterior.
O ponto 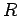 é evidentemente o
ponto de intersecção das rectas de coordenadas paralelas é evidentemente o
ponto de intersecção das rectas de coordenadas paralelas
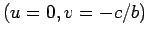 e e 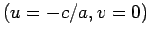 , que correspondem
aos pontos de
intersecção da recta , que correspondem
aos pontos de
intersecção da recta 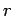 com os eixos com os eixos 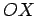 e e 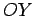 ,
respectivamente. ,
respectivamente.
Para demonstrar a proposição anterior, e também
para localizar
a posição dos pontos em 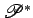 , consideremos um referencial , consideremos um referencial 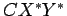 , no plano , no plano 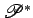 ,
como se indica no applet anterior. ,
como se indica no applet anterior.
Neste referencial, a recta 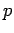 , de coordenadas paralelas , de coordenadas paralelas 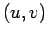 ,
é a recta que une os pontos ,
é a recta que une os pontos 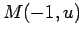 e e 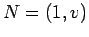 , e portanto tem
por equação: , e portanto tem
por equação:
Mas:
(substituímos a segunda linha
pela que se obtem multiplicando-a por 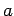 e somando-a à terceira
linha multiplicada por e somando-a à terceira
linha multiplicada por 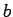 ). Como ). Como 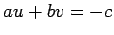 , concluímos
que a
recta passa sempre pelo ponto , concluímos
que a
recta passa sempre pelo ponto 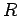 de coordenadas: de coordenadas:
que são portanto
as coordenadas, relativas ao referencial 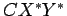 , do ponto cuja
equação tangencial é , do ponto cuja
equação tangencial é 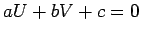 . .
Se uma curva 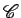 , no plano , no plano 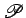 , é dada implicitamente
por: , é dada implicitamente
por:
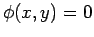 |
(20) |
a equação da recta tangente a 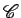 , num dos seus pontos , num dos seus pontos 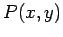 , i.e., , i.e., 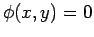 , é: , é:
isto é:
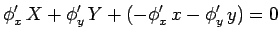 |
(21) |
onde 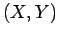 são
as coordenadas de um ponto corrente sobre essa
recta tangente, que notámos por são
as coordenadas de um ponto corrente sobre essa
recta tangente, que notámos por 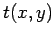 . .
Por dualidade, o ponto 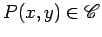 , que
verifica a
equação , que
verifica a
equação 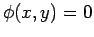 , corresponde
à recta , corresponde
à recta 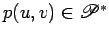 ,
onde ,
onde 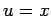 e e 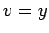 . Portanto as coordenadas . Portanto as coordenadas 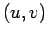 desta recta
satisfazem a equação desta recta
satisfazem a equação 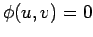 . A pontual . A pontual 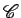 , no plano , no plano
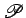 , corresponde assim a uma
família de rectas , corresponde assim a uma
família de rectas 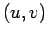 , no
plano , no
plano 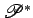 , que satisfazem a
equação , que satisfazem a
equação 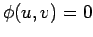 . .
Quanto
à recta tangente a 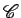 , no ponto , no ponto 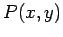 , recta que
notámos por , recta que
notámos por 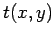 , e cuja
equação é (22),
ela corresponde por dualidade ao ponto de , e cuja
equação é (22),
ela corresponde por dualidade ao ponto de 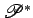 de equação: de equação:
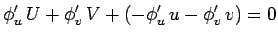 |
(22) |
Este ponto 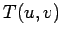 pertence à recta pertence à recta
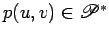 , e diz-se
o ponto característico dessa recta. O ponto , e diz-se
o ponto característico dessa recta. O ponto 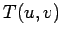 descreve pois uma pontual
descreve pois uma pontual 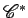 , no plano , no plano 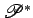 , a que
chamámos a curva dual à curva , a que
chamámos a curva dual à curva 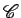 e que não é mais do
que
a envolvente da família de rectas e que não é mais do
que
a envolvente da família de rectas 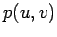 . A curva dual pode
reduzir-se a um ponto, como por exemplo acontece
quando se . A curva dual pode
reduzir-se a um ponto, como por exemplo acontece
quando se  é uma recta em é uma recta em 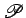 . .
No applet seguinte pode
apreciar a descrição pontual de uma
cónica (uma elipse) em  e a decrição tangencial da
cónica
dual em e a decrição tangencial da
cónica
dual em 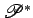 . Pode variar com o rato a
configuração da
cónica. . Pode variar com o rato a
configuração da
cónica.
Next: Nomogramas
de alinhamento
Previous: Nomogramas
rectílineos
Índice
Joao Nuno Tavares
2005-03-28
|
|
|
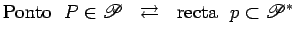
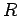 . Simbòlicamente:
. Simbòlicamente:
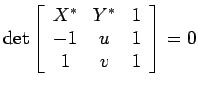
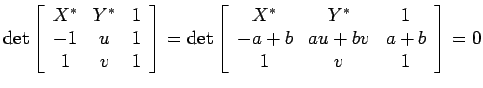
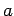 e somando-a à terceira
linha multiplicada por
e somando-a à terceira
linha multiplicada por 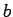 ). Como
). Como 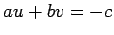 , concluímos
que a
recta passa sempre pelo ponto
, concluímos
que a
recta passa sempre pelo ponto 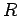 de coordenadas:
de coordenadas: 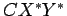 , do ponto cuja
equação tangencial é
, do ponto cuja
equação tangencial é 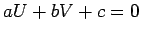 .
.
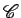 , num dos seus pontos
, num dos seus pontos 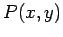 , i.e.,
, i.e., 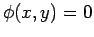 , é:
, é: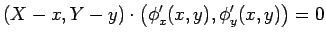
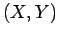 são
as coordenadas de um ponto corrente sobre essa
recta tangente, que notámos por
são
as coordenadas de um ponto corrente sobre essa
recta tangente, que notámos por 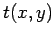 .
.
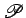 e
e 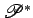 . Uma dualidade ou
correlação entre eles é uma correspondência
do tipo:
. Uma dualidade ou
correlação entre eles é uma correspondência
do tipo: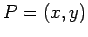
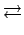
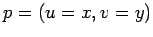
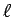
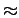 ponto suporte
ponto suporte 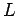
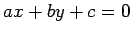
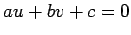
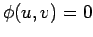
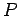
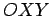 , e no plano
, e no plano 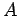 e
e
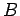 . Ao ponto
. Ao ponto 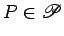 , de coordenadas
, de coordenadas 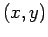 , associámos a
recta
, associámos a
recta 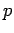 , de
, de 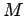 e
e 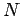 , onde
, onde 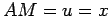 e
e
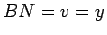 (ambos
marcados de acordo com a orientação definida em
cada recta).
(ambos
marcados de acordo com a orientação definida em
cada recta). 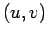 dizem-se as coordenadas
paralelas da recta
dizem-se as coordenadas
paralelas da recta
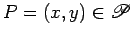 percorre a recta
percorre a recta 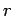 de
de
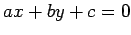
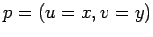 , em
, em 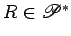 .
.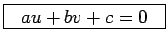
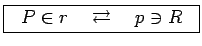
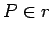 para constatar o
significado da proposição anterior.
para constatar o
significado da proposição anterior. 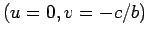 e
e 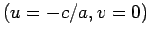 , que correspondem
aos pontos de
intersecção da recta
, que correspondem
aos pontos de
intersecção da recta 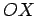 e
e 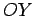 ,
respectivamente.
,
respectivamente. 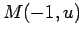 e
e 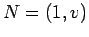 , e portanto tem
por equação:
, e portanto tem
por equação:
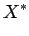
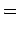
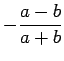
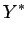
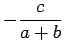
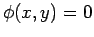
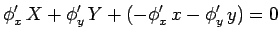
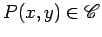 , que
verifica a
equação
, que
verifica a
equação 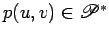 ,
onde
,
onde 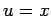 e
e 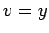 . Portanto as coordenadas
. Portanto as coordenadas 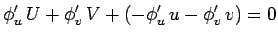
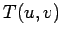 pertence à recta
pertence à recta
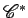 , no plano
, no plano  . A curva dual pode
reduzir-se a um ponto, como por exemplo acontece
quando se
. A curva dual pode
reduzir-se a um ponto, como por exemplo acontece
quando se