| O que é a Nomografia? |
||
| Next: Outro exemplo: a
equação Up: Nomogramas de alinhamento Previous: Nomogramas de alinhamento
Índice |
||
|
Transformemos por dualidade o nomograma da equação cúbica definido pontualmente no plano  , pelas famílias de rectas: , pelas famílias de rectas:
Relativamente às coordenadas paralelas 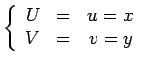 que são as rectas
 e e  , respectivamente.
A terceira família representa uma família de rectas
(não
paralelas) - para cada , respectivamente.
A terceira família representa uma família de rectas
(não
paralelas) - para cada 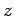 temos a recta de equação temos a recta de equação 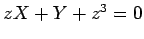 , no plano , no plano 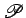 , a que
corresponde por dualidade o ponto, de , a que
corresponde por dualidade o ponto, de 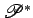 , de equação: , de equação: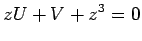
Quando
Recordemos que cada ponto do plano
Por dualidade, a descrição correspondente no plano 
Next: Outro exemplo: a equação Up: Nomogramas de alinhamento Previous: Nomogramas de alinhamento Índice Joao Nuno Tavares 2005-03-28 |
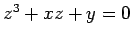
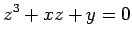
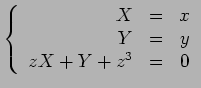
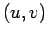 , as duas
primeiras famílias correspondem por dualidade às duas
pontuais
no plano
, as duas
primeiras famílias correspondem por dualidade às duas
pontuais
no plano  , em
, em 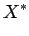
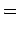
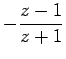
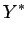
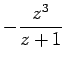
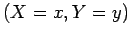 ,
representava a equação do terceiro grau, em
,
representava a equação do terceiro grau, em 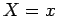 e
e 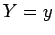 , das duas primeiras
famílias, representa a equação
, das duas primeiras
famílias, representa a equação 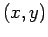 .
. 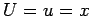 e
e 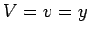 , das duas
primeiras famílias de pontuais, isto é, a recta
, das duas
primeiras famílias de pontuais, isto é, a recta 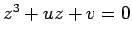 . As
soluções desta equação são dadas
pelos valores de
. As
soluções desta equação são dadas
pelos valores de