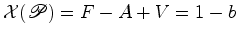Fórmula de Euler
Consideremos
uma figura plana 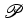 poligonal simples (sem
"buracos"), constituída por polígonos (faces), em
número
finito, colados pelas respectivas arestas, de tal forma que duas
faces quaisquer, quando se intersectam, o fazem, ou segundo um
vértice comum, ou segundo uma aresta comum.
poligonal simples (sem
"buracos"), constituída por polígonos (faces), em
número
finito, colados pelas respectivas arestas, de tal forma que duas
faces quaisquer, quando se intersectam, o fazem, ou segundo um
vértice comum, ou segundo uma aresta comum.
Eis um exemplo:
|
||||
|
Se
A
expressão |
||||
|
Eis uma demostração que se deve a Cauchy:
Para a figura poligonal anterior temos, por exemplo, a seguinte sequência: |
||||
Se 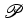 contiver buracos poligonais, a sua
característica será
também igual a 1
? O exemplo seguinte mostra que tal não acontece (verifique!). contiver buracos poligonais, a sua
característica será
também igual a 1
? O exemplo seguinte mostra que tal não acontece (verifique!). |
||||
|
Mas
podemos generalizar a fórmula de Euler para figuras planas
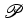 poligonais com poligonais com 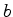 "buracos"
poligonais. Designemos mais
uma vez por "buracos"
poligonais. Designemos mais
uma vez por 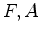 e e 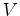 , respectivamente o número de faces,
arestas e vértices de
, respectivamente o número de faces,
arestas e vértices de 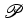 .
. Consideremos
agora a figura Para esta nova figura temos portanto que: 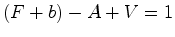
que é a fórmula de Euler generalizada para figuras planas 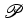 poligonais com
poligonais com 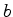 "buracos" poligonais.
"buracos" poligonais. |
||||
| Seguinte: O teorema de
Pick e a fórmula de Euler Anterior:O teorema de Pick Regresso ao Índice |
||||
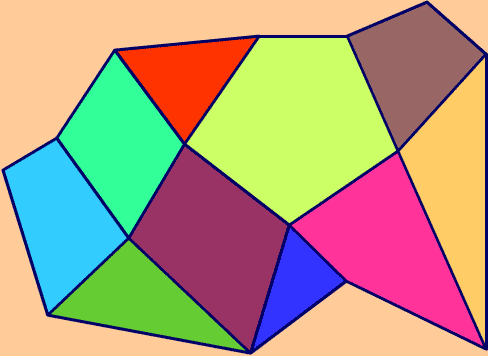
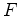 representa o número de faces,
representa o número de faces, 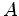 o número de arestas e
o número de arestas e 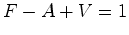
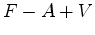 designa-se por característica
de
Euler de
designa-se por característica
de
Euler de 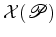 . Deste modo, a
característica de Euler de uma figura plana poligonal simples
(sem "buracos"), é igual a 1.
. Deste modo, a
característica de Euler de uma figura plana poligonal simples
(sem "buracos"), é igual a 1. 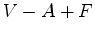 mantem-se
inalterada.
mantem-se
inalterada.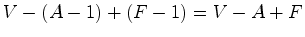
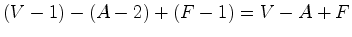
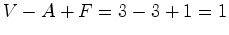
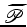 , que se obtem a partir
de
, que se obtem a partir
de 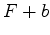 , enquanto que o
número de arestas e de
vértices continua
o mesmo -
, enquanto que o
número de arestas e de
vértices continua
o mesmo -