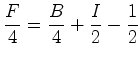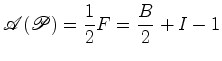Relação entre o teorema de Pick e a fórmula de Euler
|
Seguidamente, vamos ver a equivalência entre o
teorema de Pick e
a
fórmula de Euler. Para tal precisamos do conceito seguinte: Definição
Um triângulo diz-se
primitivo, ou fundamental, se os seus únicos pontos de
coordenadas inteiras são os vértices.
|
||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||
Demonstração...
Seja  uma figura poligonal
simples,
com uma figura poligonal
simples,
com  vértices (em pontos de coordenadas inteiras),
vértices (em pontos de coordenadas inteiras), 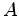 arestas e
arestas e 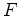 faces.
faces.
Triangulemos
|
||||||||||||||||||||||||||||||||||||
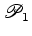 tem mais uma
face, mais duas arestas e mais um vértice do que
tem mais uma
face, mais duas arestas e mais um vértice do que 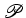 , e,
portanto:
, e,
portanto:
como se tinha afirmado. Podemos pois supôr
que O
que pretendemos provar é que
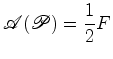 Pelo teorema de Pick, temos então que: Por
outro lado, sabemos que
cada face de
Mas
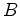 é
o número de vértices na fronteira, portanto igual ao
número de
arestas na fronteira. Por outro lado, é claro que o
número de
arestas interiores é igual ao número total de arestas, é
o número de vértices na fronteira, portanto igual ao
número de
arestas na fronteira. Por outro lado, é claro que o
número de
arestas interiores é igual ao número total de arestas, 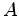 ,
menos o número de arestas de fronteira.
,
menos o número de arestas de fronteira. Reunindo todas estas
informações, vem que: Atendendo a que
como se pretendia mostrar. |
||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||
|
Demonstração...
Consideremos mais uma vez uma figura poligonal simples,
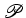 , com , com 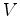 vértices
(em pontos de coordenadas
inteiras), vértices
(em pontos de coordenadas
inteiras), 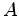 arestas e arestas e 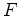 faces, que supômos
triangulada em faces, que supômos
triangulada em 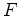 triângulos primitivos.
triângulos primitivos. Como já sabemos: 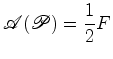 Usando a fórmula de Euler,
Logo:
que é o teorema de Pick. |
||||||||||||||||||||||||||||||||||||
| Seguinte: Uma prova de
Descartes Anterior: A fórmula de Euler Regresso ao Índice |

 mantem-se inalterada. A prova
destes factos faz-se por indução. De facto, procedendo ao
primeiro
passo da triangulação de
mantem-se inalterada. A prova
destes factos faz-se por indução. De facto, procedendo ao
primeiro
passo da triangulação de 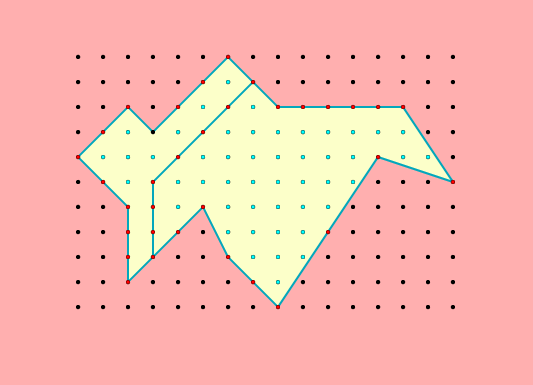
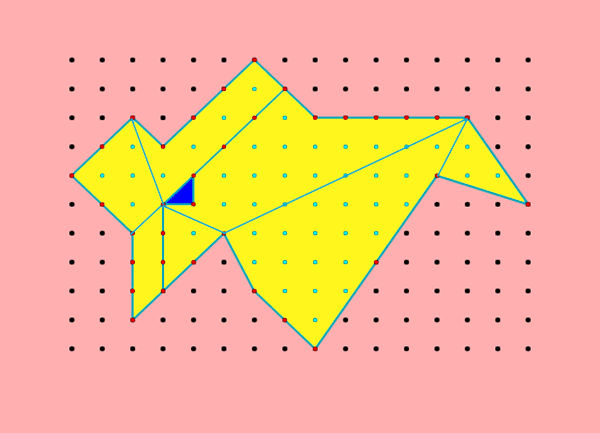
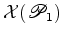
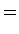
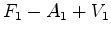
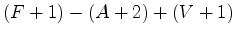
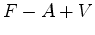
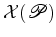
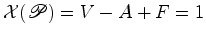 , supondo
verdadeiro o teorema de Pick:
, supondo
verdadeiro o teorema de Pick: 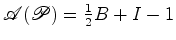 .
. 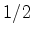 ,
a área de
,
a área de 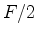 :
: 
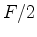
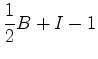
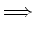
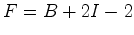

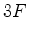
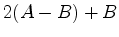
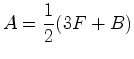
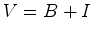 e às igualdades (
e às igualdades (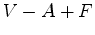

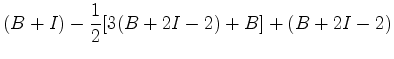
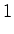
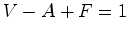 , a igualdade
(
, a igualdade
(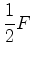
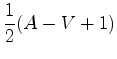
![$\displaystyle \frac{1}{2}\left[\frac{1}{2}(3 F+B)-(B+I)+1\right]$](img98.gif)