Uma prova de Descartes
|
Usando o facto de que um
triângulo primitivo tem área 1/2 e
uma ideia de Descartes podemos deduzir simultâneamnete o teorema
de Pick e a fórmula de Euler.
Demonstração ... Supômos
mais uma vez
que Se somarmos todos os
ângulos internos de todas as faces de
Façamos a mesma soma,
mas agora adicionando os
ângulos
vértice a vértice.
Claro que em cada
vértice
interior temos Concluindo:
Portanto:
que é o teorema de Pick. Por outro lado, as igualdades (9)
e (7),
respectivamente, 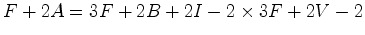 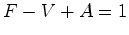 |
|||||||||||||||||||||
| Seguinte:
Extensão do teorema de Pick Anterior: Teorema de Pick e a fórmula de Euler Regresso ao Índice |
|||||||||||||||||||||
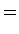
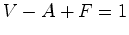

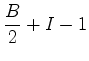
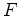 triângulos primitivos, de tal forma que
triângulos primitivos, de tal forma que 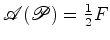 .
. 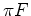 radianos.
radianos.
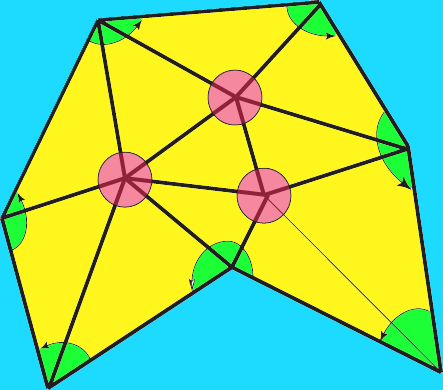
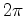 radianos e, portanto, a
contribuição
total dos vértices
interiores é
radianos e, portanto, a
contribuição
total dos vértices
interiores é  . Restam os ângulos em vértices de
fronteira. Mas estes ângulos são os ângulos internos
de um
polígono com
. Restam os ângulos em vértices de
fronteira. Mas estes ângulos são os ângulos internos
de um
polígono com 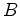 arestas. Logo a sua soma
é
arestas. Logo a sua soma
é 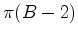 .
. 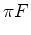
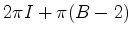
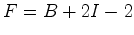
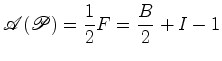
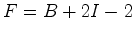 e
e 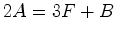 , implicam que:
, implicam que: