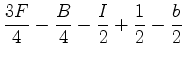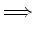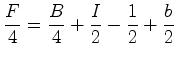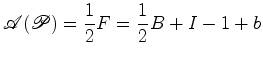Extensão do Teorema de Pick
| Até agora, usámos o teorema de Pick apenas para o cálculo de áreas de polígonos simples. Vamos agora generalizar esse teorema para polígonos com buracos. | ||||||||||||||||||||||
|
||||||||||||||||||||||
Eis um exemplo: 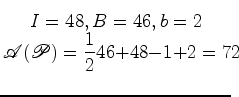 |
||||||||||||||||||||||
Demonstração...
Supômos que 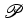 está triangulada em está triangulada em 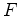 triângulos
primitivos, de tal forma que
triângulos
primitivos, de tal forma que 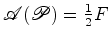 .
.
Recordemos que a
fórmula de Euler generalizada para figuras
planas
Usando esta fórmula de Euler, a igualdade (9), e
ainda o facto de que
e portanto:
como se pretendia. |
||||||||||||||||||||||
| Seguinte:
Uma aplicação aritmética do teorema de Pick Anterior: Extensão do teorema de Pick Regresso ao Índice |
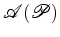
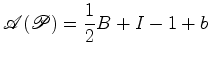
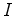
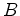
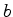
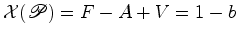
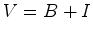 , obtemos:
, obtemos: 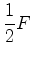
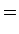
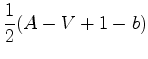
![$\displaystyle \frac{1}{2}\left[\frac{1}{2}(3 F+B)-(B+I)+1-b\right]$](img118.gif)