E em dimensão 3 ? Será válido o teorema de Pick?
|
O conceito de reticulado tridimensional faz todo o
sentido - é
constituído por todos os pontos É então natural questionarmo-nos se existe
uma
fórmula de Pick
para calcular o volume de um poliedro tridimensonal, cujos
vértices pertençam ao reticulado, em termos dos pontos
desse
reticulado interiores e na fronteira do poliedro. Esta é uma questão muito mais difíl de responder. De facto, não existe uma fórmula simples que resolva o problema, como podemos constatar através do exemplo seguinte:
Exemplo
...
para cada inteiro
Os únicos pontos do reticulado que pertencem a cada um destes tetraedros são os seus quatro vértices. O problema é que, quando variamos a altura Aqui está um bom problema para
investigação! Veja o artigo de J.
E. Reeve, citado na bibliografia. |
||
|
|
||
|
Bibliografia
|
||
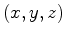 de
coordenadas inteiras.
de
coordenadas inteiras. 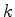 , consideremos o tetraedro cuja base é o triângulo no
plano
, consideremos o tetraedro cuja base é o triângulo no
plano 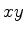 de
vértices
de
vértices 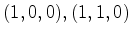 e
e 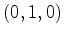 , e com quarto vértice no ponto
, e com quarto vértice no ponto 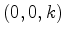 :
: 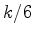 ).
).