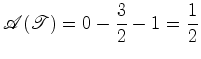Uma aplicação aritmética do teorema de Pick
|
|
||||
|
Exemplos:
(i). se 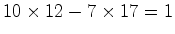 (ii). Um outro exemplo: se 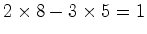 |
||||
|
Não se conhece uma
fórmula simples para calcular
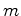 e e 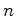 , em
função de
, em
função de 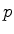 e e 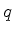 , embora exista um processo sistemático - o
algoritmo de Euclides - que pode ser aplicado a cada par
, embora exista um processo sistemático - o
algoritmo de Euclides - que pode ser aplicado a cada par 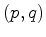 para determinar uma solução
para determinar uma solução 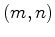 da
equação
(20). da
equação
(20). É neste contexto que o teorema de Pick pode ser útil. Vejamos como. Dado um par de inteiros Mova-se agora esta recta,
paralelamente a si própria,
até
encontrar, pela primeira vez, um ponto Na figura seguinte,
ilustra-se o método para
Consideremos
agora o
triângulo de acordo com o teorema de Pick. Mas, por outro lado, essa mesma área é igual a: De facto, a figura seguinte mostra que a área de um triângulo de vértices 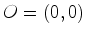 , , 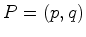 e e 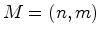 , mesmo que não seja
prmitivo, é igual a , mesmo que não seja
prmitivo, é igual a 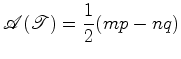 (verifique isto!). (verifique isto!).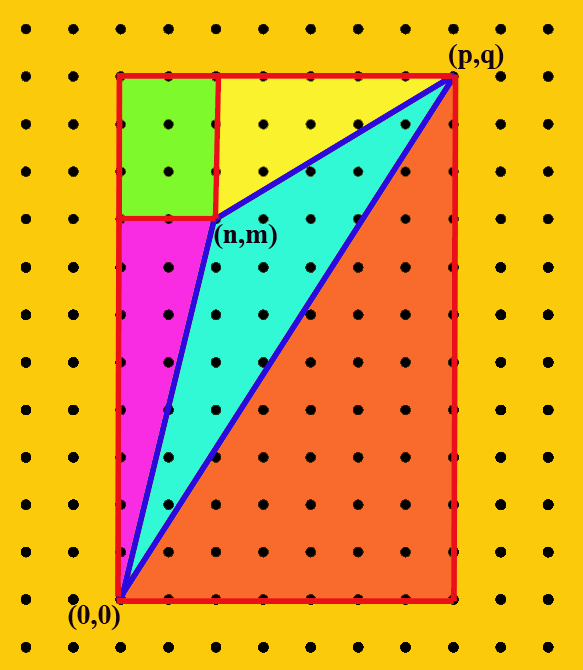 |
||||
|
Igualando (21) e (22),
obtemos: 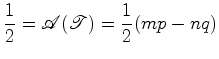
Desta forma obtemos pois uma solução para o problema proposto. |
||||
| Seguinte: E em
dimensão 3? Será válido o teorema de Pick? Anterior: Uma aplicação aritmética do teorema de Pick Regresso ao Índice |
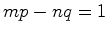
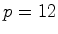 e
e 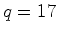 , podemos tomar
, podemos tomar 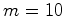 e
e 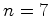 . De
facto:
. De
facto: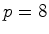 e
e 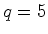 , podemos tomar
, podemos tomar 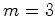 e
e 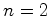 . De
facto:
. De
facto: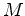 do reticulado.
Designemos
por
do reticulado.
Designemos
por 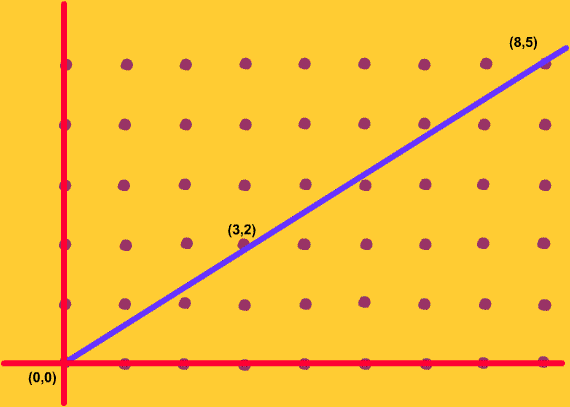
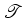 com vértices
com vértices 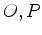 e
e