Nonlinear IDE

Example 1

Let us consider the nonlinear integro-differential equation \begin{equation*} \begin{cases} \displaystyle\frac{d}{dx}y +y -\int_{0}^{1}y(t) ^2dt=0.5(e^{-2}-1)\\ y(0) =1 \end{cases}. \label{non_lin_ideF} \end{equation*} Its linearizaition with auxilar variable produces $$ \begin{cases} \displaystyle\frac{d}{dx}y_1^{(k+1)}+y_1^{(k+1)}-\int_{0}^{1}y_2^{(k+1)}dt=0.5(e^{-2}-1)\\ \displaystyle\frac{d}{dx}y_2^{(k+1)}-2\left(y_1^{(k)}\frac{d}{dx}y_1^{(k+1)}+\frac{d}{dx}y_1^{(k)}y_1^{(k+1)}\right)=-2y_1^{(k)}\frac{d}{dx}y_1^{(k)}\\ y_1^{(1)}(0)=1,\quad y_2^{(1)}(0)=1 \end{cases}. $$ The approximate solution on Tau Toolbox:

The approximate tau solution achieves the machine precision: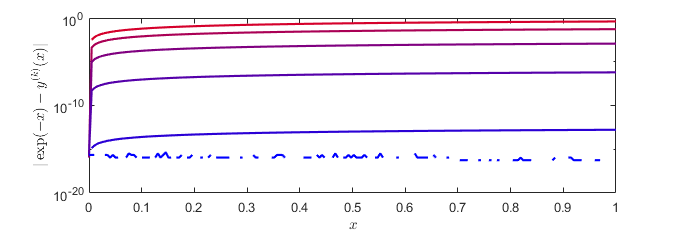
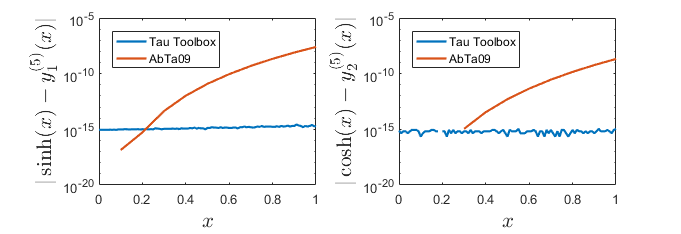
Example 2

Let us consider the nonlinear system of integro-differential equations \begin{equation*} \begin{cases} \displaystyle \frac{d}{dx}y_1 +\frac{1}{2}{{\left(\frac{d}{dx}y_2 \right)^2}}-\int_{0}^{x}(x-t)y_2(t)+{{y_2(t)y_1(t)}}dt=1\\ \displaystyle \frac{d}{dx}y_2 -\int_{0}^{x}(x-t)y_1(t)-{{y_2^2(t)}}+{{y_1^2(t)}}dt=2x\\ \displaystyle y_1(0)=0,\quad y_2(0)=1 \end{cases}. \end{equation*} Its linearization produces \begin{equation*} \label{iter_inter_non_lin_ideV} \begin{cases} \displaystyle\frac{d}{dx}y_1^{(k+1)}+\frac{d}{dx}y_2^{(k)}\frac{d}{dx}y_2^{(k+1)}-\int_{0}^{x}y_2^{(k+1)}dt-\int_{0}^{x}y_5^{(k+1)}dt=1+0.5\left(\frac{d}{dx}y_2^{(k)}\right)^2\\ \displaystyle \frac{d}{dx}y_2^{(k+1)}-\int_{0}^{x}(x-t)y_1^{(k+1)}dt-\int_{0}^{x}y_3^{(k+1)}-y_4^{(k+1)}dt=2x\\ \displaystyle \frac{d}{dx}y_3^{(k+1)}-2\left(\frac{d}{dx}y_1^{(k)}y_1^{(k+1)}+y_1^{(k)}\frac{d}{dx}y_1^{(k+1)}\right)=-2y_1^{(k)}\frac{d}{dx}y_1^{(k)}\\ \displaystyle \frac{d}{dx}y_4^{(k+1)}-2\left(\frac{d}{dx}y_2^{(k)}y_2^{(k+1)}+y_2^{(k)}\frac{d}{dx}y_2^{(k+1)}\right)=-2y_2^{(k)}\frac{d}{dx}y_2^{(k)}\\ \displaystyle \frac{d}{dx}y_5^{(k+1)}-y_1^{(k)}\frac{d}{dx}y_2^{(k+1)}-\frac{d}{dx}y_1^{(k)}y_2^{(k+1)}-\frac{d}{dx}y_2^{(k)}y_1^{(k+1)}-y_2^{(k)}\frac{d}{dx}y_1^{(k+1)}=\\\displaystyle\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad=-y_1^{(k)}\frac{d}{dx}y_2^{(k)}-\frac{d}{dx}y_1^{(k)}y_2^{(k)}\\ y_1^{(1)}(0)=0,\quad y_2^{(1)}(0)=1,\quad y_3^{(1)}(0)=0,\quad y_4^{(1)}(0)=1,\quad y_5^{(1)}(0)=0\quad \end{cases}. \end{equation*} The approximate solution on Tau Toolbox:

The approximate tau solution achieves the machine precision (comparison with the paper Abbasbandy and A. Taati - Numerical solution of the system of nonlinear Volterra integro-differential equations with nonlinear differential part by the operational tau method and error estimation - 2009 is presented):