Systems of ODE
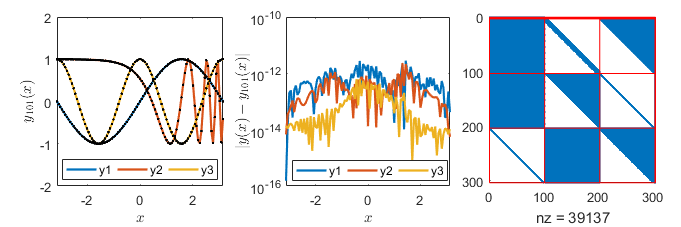
Example 1Let us consider the linear system of differential equations with polynomial coefficients $$ \begin{cases} \displaystyle y_2-\frac{d}{dx}y_1=0\\ \displaystyle y_3-\frac{d}{dx}y_2=0\\ \displaystyle (x^2+1)\frac{d}{dx}y_3-(x^2+3x)\frac{d}{dx}y_2+5xy_2-5y_1=60x^2-10\\ y_1(-1)=4,\ y_2(1)=2,\ y_3(0)=0 \end{cases}. $$ The approximate solution on Tau Toolbox:
Example 2
Let us consider the linear system of differential equations with non-polynomial coefficients $$ \begin{cases} \displaystyle \cos(x)\frac{d}{dx}y_1-(x^2-3x^4)y_2+3\frac{d}{dx}y_3 = \cos(x)^2-\cos(\exp(x))(- 3x^4+x^2)-6\sin(2x)\\ \displaystyle \sin(x)\frac{d}{dx}y_1+\frac{d}{dx}y_2-y_3 =\sin(x)\cos(x)-\cos(2x)-\sin(\exp(x))\exp(x)\\ \displaystyle -y_1+\exp(x)y_2+x^3\frac{d}{dx}y_3 =\cos(\exp(x))\exp(x) - \sin(x) - 2x^3\sin(2x)\\ y_1(-\pi)=0,\ y_2(0)=\cos(1),\ y_3(\pi)=1 \end{cases} $$ The approximate solution on Tau Toolbox: