Nonlinear ODE
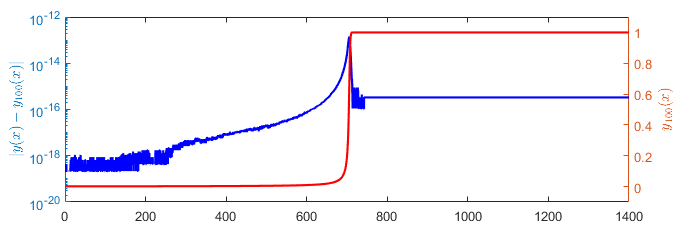
Example 1Let us consider the nonlinear differential equation $$ \begin{cases} \displaystyle \frac{d}{dx}y+y^2(y-1)=0,\ x\in\left]0,\ \frac{2}{\delta}\right[\\ y(0)=\delta \end{cases},\ \delta>0. $$ Its exact solution is $y = \left(W\left(\left(\frac{1}{\delta}-1\right)e^{\frac{1}{\delta}-1 - x}\right) + 1\right)^{-1}$, where $W(z)$ is the W Lambert function solution of $W(z)e^{W(z)} = z$. The approximate solution on Tau Toolbox is obtained writing:
Example 1
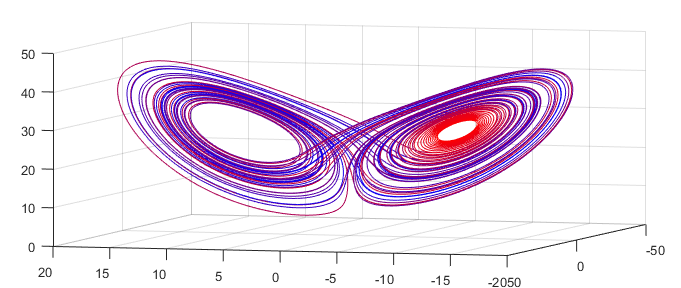
Let us consider the nonlinear system of differential equations $$ \begin{cases} \displaystyle \frac{d}{dt}y_1 - \sigma\left(y_2 - y_1\right) = 0\\ \displaystyle\frac{d}{dt}y_2 - \rho y_1 + y_1y_3 + y_2 = 0\\ \displaystyle\frac{d}{dt}y_3 - y_1y_2 + \beta y_3 = 0\\ y_1(t_0)=y_{10},\quad y_2(t_0)=y_{20},\quad y_3(t_0)=y_{30} \end{cases}. $$ Its linearization produces $$ \begin{cases} \displaystyle \frac{d}{dt}y_1^{(k+1)}-\sigma\left(y_2^{(k+1)}-y_1^{(k+1)}\right)=0\\ \displaystyle \frac{d}{dt}y_2^{(k+1)}-\rho y_1^{(k+1)}+y_1^{(k)}y_3^{(k+1)}+y_3^{(k)}y_1^{(k+1)}+y_2^{(k+1)}=y_1^{(k)}y_3^{(k)}\\ \displaystyle\frac{d}{dt}y_3^{(k+1)}-y_1^{(k)}y_2^{(k+1)}-y_2^{(k)}y_1^{(k+1)}+\beta y_3^{(k+1)}=-y_1^{(k)}y_2^{(k)}\\ y_1^{(1)}(t_0)=y_{10},\quad y_2^{(1)}(t_0)=y_{20},\quad y_3^{(1)}(t_0)=y_{30} \end{cases}. $$ The approximate solution on Tau Toolbox: